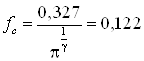Промышленность производство : Курсовая работа: Расчет вихревого холодильно-нагревательного аппарата
Курсовая работа: Расчет вихревого холодильно-нагревательного аппарата
Курсовой
проект
по дисциплине
Термодинамика
технических устройств
на тему:
“Расчет
вихревого холодильно-нагревательного аппарата”
Задание
Спроектировать систему
термостатирования электронных устройств.
Технические условия
работы системы: температура в камере термостатирования 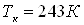 , холодопроизводительность , холодопроизводительность 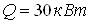 . Давление и температура
сжатого газа на входе в систему (магистральные параметры) . Давление и температура
сжатого газа на входе в систему (магистральные параметры) 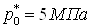 , , 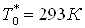 . Необходимый объем
термокамеры и ее геометрия. . Необходимый объем
термокамеры и ее геометрия.
Требуется произвести:
1)
выбор или
создание принципиальной схемы работы термостата;
2)
тепловой расчет
режимных характеристик схемы (температур в заданных сечениях схемы, расходных
соотношений, эффективности);
3)
термодинамический
анализ схемы и его узлов. Определение оптимальных режимов работы схемы;
4)
расчет потрубных
значений расхода воздуха.
Содержание
Список условных обозначений
Введение
Расчетная часть
1 Принцип действия установки
2 Определение оптимальных режимов работы схемы
2.1 Теплообменные аппараты 5
2.2 Противоточная вихревая труба 3
2.3 Охлаждаемый объект 2
2.4 Подогреваемый объект 1
2.5 Двухконтурная вихревая труба 4
2.6 Эжектор 6
3 Расчет потребного количества сжатого воздуха
4 Расчет эжектора
5 Расчет эксергии потоков в элементах схемы термостата
6 Геометрические параметры ВХНА
Заключение
Список использованных источников
Список
условных обозначений
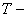 температура, температура, 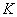 ; ;
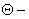 относительная температура; относительная температура;
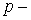 давление, давление, 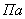 ; ;
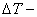 изменение температуры, изменение температуры, 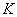 ; ;
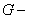 расход, расход, 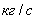 ; ;
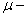 относительная доля охлажденного
потока; относительная доля охлажденного
потока;
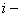 энтальпия, энтальпия, 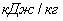 ; ;
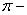 степень расширения воздуха; степень расширения воздуха;
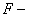 площадь, площадь, 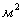 ; ;
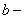 ширина, ширина, 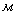 ; ;
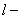 длина, длина, 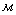 ; ;
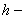 высота, высота, 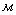 ; ;
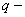 теплонапряженность установки, теплонапряженность установки, 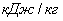 ; ;
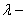 теплопроводность, теплопроводность, 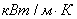 ; ;
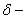 толщина изоляции, толщина изоляции, 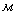 ; ;
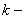 коэффициент запаса по сжатому
воздуху; коэффициент запаса по сжатому
воздуху;
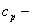 изобарная теплоемкость, изобарная теплоемкость, 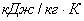 ; ;
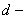 диаметр, диаметр, 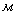 ; ;
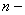 коэффициент эжекции; коэффициент эжекции;
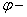 адиабатный КПД, адиабатный КПД, 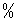 ; ;
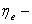 эксергетический КПД, эксергетический КПД, 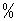 ; ;
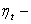 термический КПД, термический КПД, 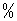 ; ;
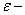 холодильный коэффициент; холодильный коэффициент;
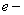 эксергия, эксергия, 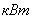 ; ;
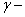 показатель адиабаты; показатель адиабаты;
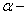 геометрический параметр; геометрический параметр;
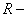 газовая постоянная, газовая постоянная, 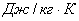 ; ;
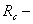 радиус сопряжения, радиус сопряжения, 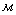 . .
Надстрочные индексы
* – параметры торможения.
Подстрочные индексы
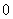 – магистральные параметры; – магистральные параметры;
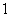 – параметры подогреваемого объекта; – параметры подогреваемого объекта;
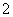 – параметры охлаждаемого объекта; – параметры охлаждаемого объекта;
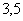 – параметры теплообменных аппаратов; – параметры теплообменных аппаратов;
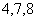 – параметры вихревых труб с
дополнительным потоком; – параметры вихревых труб с
дополнительным потоком;
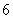 – параметры эжектора; – параметры эжектора;
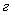 – параметры подогретого потока; – параметры подогретого потока;
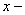 параметры охлажденного потока; параметры охлажденного потока;
д – параметры
дополнительного потока;
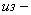 параметры изоляции; параметры изоляции;
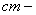 параметры стенки; параметры стенки;
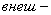 внешние параметры; внешние параметры;
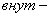 внутренние параметры; внутренние параметры;
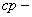 средние параметры; средние параметры;
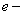 эксергетический; эксергетический;
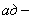 адиабатный; адиабатный;
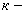 камера; камера;
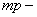 труба; труба;
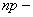 параметры привода; параметры привода;
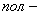 полные параметры; полные параметры;
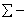 суммарный; суммарный;
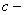 сопло. сопло.
Введение
В
настоящее время все более актуальной становится проблема энергетического
обеспечения жизни общества. Энергетические кризисы, поражают время от времени
различные регионы из-за снижения добычи энергоносителей или их дорогостоящей
транспортировки к месту использования. Возникают экологические проблемы,
связанные с негативным влиянием выбросов при сжигании топлива и его
переработкой и хранением. Недостаток энергоресурсов связан с тем, что запасы
органических топлив - нефти, газа, угля, истощаются и не возобновляются.
Поэтому удовлетворение потребностей общества в энергии возможно при комплексном
решении проблем энергетики. В связи с ограниченностью запасов энергоносителей
важными становятся вопросы их эффективного использования и создания
энергетических установок с высоким коэффициентом использования топлива,
тепловым коэффициентом и КПД. Экономия топлива и сопутствующих материалов -
главная задача этого направления развития энергетики. Современные технологии
использования возобновляемых энергетических ресурсов недостаточно эффективны
или дороги по сравнению с технологиями преобразования энергии органических
топлив. Анализ современных энергетических технологий, показывает, что один из
перспективных - способ преобразования тепловой энергии на основе вихревого
эффекта, который выгодно отличается от известных устройств простотой
технического выполнения и обслуживания, а также является более дешевым в
промышленном производстве. Вихревые трубы безопасны, компактны и надежны в
промышленнойэксплуатации.
Применение
вихревой трубы в различных технологиях целесообразно при наличии неиспользуемой
энергии перепадов давления для очистки и охлаждения любых газов и газовых
смесей в том числе содержащих жидкие и конденсирующиеся примеси. Так,
в южных городах существует проблема - из-за высокой температуры воздуха из
крана для холодной воды течет отнюдь не холодная, а теплая вода и в начале 90-х
годов исследователи решили использовать вихревую трубу для разделения воды на
горячую и холодную. Результаты оказались сенсационными. Температура вращающейся
в трубе воды повышалась, будто ее согревал невидимый кипятильник.
Работа
вихревой трубы заключается в создании сверхзвукового закрученного потока газа и
последующего его разделения на холодный и горячий (или тёплый) потоки,
образующиеся в результате проявления вихревого эффекта Ранка. Особенно
эффективно вихревая труба может быть использована при добыче и транспорте газа,
когда требуется многократно снизить пластовое давление газа перед подачей в
магистральный трубопровод с 200 - 250 ат до 50 -60 ат и на
газораспределительных станциях с 20 - 35 ат до 1 - 6 ат. Дополнительная
установка достаточно простого оборудования при незначительных затратах даёт
возможность повысить выход газоконденсата из газа на 20 - 25 % и более. Другое
перспективное использование вихревой трубы основано на применении
электрогидродинамического течения газа для осуществления эффекта Ранка. Это
даёт возможность создать холодильное устройство, в котором отсутствуют
агрессивные хладагенты и компрессор. Вихревые трубы могут быть использованы как
индивидуально, так и в технологической схеме с теплообменником-рекуператором и
сепаратором. Вот насколько обширно применение вихревых труб. В настоящее время вихревая техника широко внедрена в
промышленность: вихревые управляющие клапаны в системах управления тягой
ракетных двигателей, вихревые холодильники, вихревые системы очистки, осушки
газа в газовой промышленности, вихревые системы газоподготовки для нужд
пневмо-газоавтоматики.
РАСЧЕТНАЯ ЧАСТЬ
1 Принцип действия установки
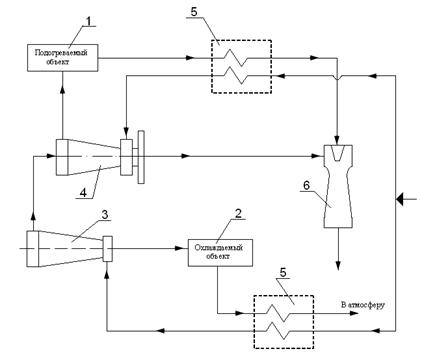
Рисунок 1.1
Принципиальная схема термостата
1 – подогреваемый объект;
2 – охлаждаемый объект; 3 – противоточная вихревая труба;
4 – двухконтурная
вихревая труба; 5 – теплообменники; 6 – эжектор.
Работа
холодильно-нагревательного аппарата осуществляется следующим образом: при
работе сжатый воздух из магистрали разделяется на два потока по числу вихревых
труб. Один из потоков сжатого воздуха, минуя теплообменник 5, подается к
сопловому устройству двухконтурной вихревой трубы 4, проходя через которую
охлаждается. Одна часть воздуха поступает в эжектор 6 в качестве эжектируемого
потока. Другая часть воздуха направляется в подогреваемый объект 1, где
нагреваясь, и минуя теплообменник 5 поступает в эжектор 6 в качестве
эжектирующего потока.
Второй поток сжатого
воздуха, проходя через теплообменник 5 поступает в противоточную вихревую
трубу3. Поток, выходящий со стороны горячего конца, поступает в двухконтурную
вихревую трубу 4. Выходя из нее часть воздуха, направляется в эжектор 6 в
качестве эжектируемого газа. Другая часть воздуха поступает в подогреваемый
объект 1, и минуя теплообменник 5 поступает в эжектор 6 в качестве
эжектирующего газа. Поток, выходя из отверстия диафрагмы противоточной вихревой
трубы 3, потсупает в охлаждаемый объект 2. Там охлаждаясь, воздух, минуя
теплообменник 5 выходит в атмосферу.
Схема термодинамического
расчета с обозначением характерных узлов и сечений представлена на рисунке 1.2.
Принятые допущения:
– гидравлические
сопротивления в такте установки не существенны;
– изобарная теплоемкость
газа в рабочем интервале температур принимается постоянной 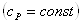 ; ;
– давление холодного
потока считается равным давлению среды, в которую происходит истечение;
– в виду малых скоростей
в рассматриваемых сечениях расчеты производятся по параметрам торможения.
Для расчета выбираются
трубы с относительной длиной камеры энергоразделения 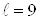 . Значение эффектов охлаждения
противоточной вихревой трубы в зависимости от степени расширения сжатого
воздуха . Значение эффектов охлаждения
противоточной вихревой трубы в зависимости от степени расширения сжатого
воздуха  и доли охлажденного потока и доли охлажденного потока
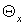 сведены в таблице 1. сведены в таблице 1.
Таблица 1.1
|
|

|
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,86 |
0,88 |
0,9 |
|
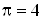
|
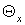
|
0,852 |
0,86 |
0,87 |
0,882 |
0,896 |
0,912 |
0,937 |
0,934 |
0,942 |
|

|
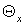
|
0,828 |
0,841 |
0,855 |
0,871 |
0,889 |
0,91 |
0,925 |
0,932 |
0,94 |
|
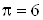
|
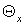
|
0,8 |
0,924 |
0,943 |
0,862 |
0,883 |
0,906 |
0,922 |
0,928 |
0,937 |
Значение относительной
доли охлажденного потока 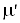 и
эффектов охлаждения вихревой трубы с дополнительным потоком и
эффектов охлаждения вихревой трубы с дополнительным потоком 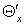 сведены в таблице 2. сведены в таблице 2.
Таблица 1.2
|
|
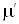
|
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
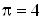
|
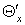
|
0,85 |
0,845 |
0,842 |
0,856 |
0,875 |
0,894 |
0,913 |
0,915 |
0,938 |
0,944 |
|

|
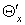
|
0,87 |
0,865 |
0,862 |
0,876 |
0,895 |
0,912 |
0,907 |
0,92 |
0,939 |
0,94 |
|
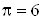
|
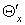
|
0,94 |
0,937 |
0,935 |
0,903 |
0,904 |
0,907 |
0,9 |
0,93 |
0,943 |
0,947 |
Схема термодинамического
расчета:
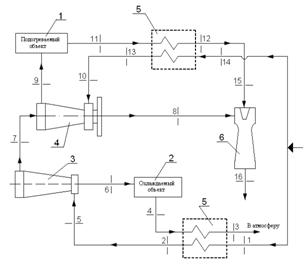
Рисунок 1.1 – Схема
термодинамического расчета
1 – подогреваемый объект;
2 – охлаждаемый объект; 3 – противоточная вихревая труба;
4 – двухконтурная
вихревая труба; 5 – теплообменники; 6 – эжектор.
2 Определение оптимальных режимов работы схемы
Основным критерием
для выбора режима работы отдельных агрегатов схамы при их совместном
использовании является достижение необходимой температуры воздуха, поступающего
в камеру климатических испытаний при максимально возможной энергетической
эффективности работы схемы.
Опишем работу отдельных
узлов аналитическими зависимостями.
2.1 Теплообменные
аппараты 5.
Рассмотрим теплообменник
5а.
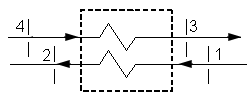
Запишем
уравнение теплового баланса для теплообменника 5а с учетом уравнения сохранения
энергии
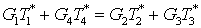
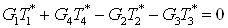
Так как 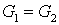 , а , а 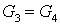 , то уравнение для теплообменника
5а примет вид , то уравнение для теплообменника
5а примет вид
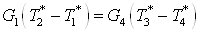 . .
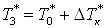 ; ;
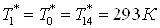 ; ;
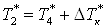 ; ;
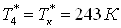 . .
Расходы найдем по
формулам:
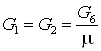 ; ;
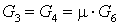 . .
Давление:
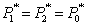 ; ;
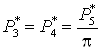
Рассмотрим теплообменник
5б.
Запишем уравнение
теплового баланса для теплообменника 5б с учетом уравнения сохранения энергии
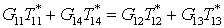
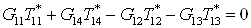
Так как 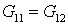 , а , а 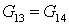 , то уравнение для
теплообменника 5а примет вид , то уравнение для
теплообменника 5а примет вид
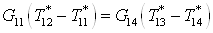 . .
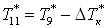 ; ;
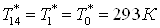 ; ;
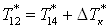 ; ;
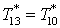 , тогда составим систему уравнений , тогда составим систему уравнений
 ; ;
 . .
Примем, что 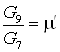 , ,  , , 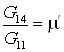 ; и зная, что ; и зная, что 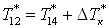 , , 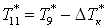 получим получим
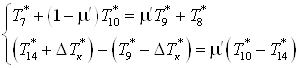 . .
Из второго выражения
системы выразим 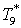 : :
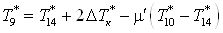 . .
Подставим получившееся
выражение для 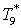 в первое
уравнение системы в первое
уравнение системы
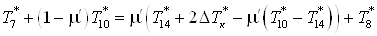 . .
Отсюда
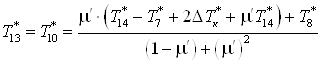 . .
Расходы определим по
формулам:
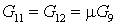 ; ;
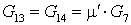 . .
Давление:
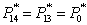 ; ;
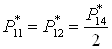
2.2 Противоточная
вихревая труба 3.
Запишем уравнение
теплового баланса с учетом уравнения сохранения энергии
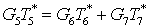 . .
Примем 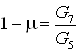 , а , а 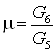 . Тогда уравнение баланса
примет вид . Тогда уравнение баланса
примет вид
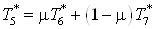 , ,
где 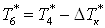 , а , а 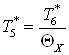 . .
Отсюда
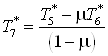 . .
Найдем расходы:
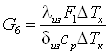 ; ;
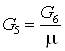 ; ;
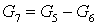 . .
Давление
; 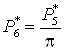 ; ; 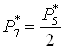
2.3 Охлаждаемый объект 2.
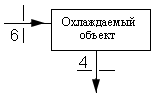
Запишем уравнение
теплового баланса с учетом уравнения сохранения энергии
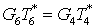 . .
Температура на выходе из
холодильной камеры
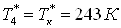 . .
Температура на выходе из
сопла противоточной вихревой трубы
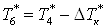 . .
Расходы
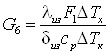 ; ;
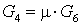 . .
Давление:
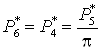 . .
2.4 Подогреваемый объект
1.
Запишем уравнение
теплового баланса с учетом уравнения сохранения энергии
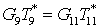 . .
Относительная доля потока
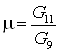 . .
Температура на входе в
подогреваемый объект
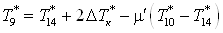 . .
Тогда температура на
выходе из объекта
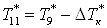 . .
Расходы
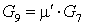 ; ;
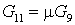 . .
Давление:
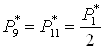
2.5 Двухконтурная
вихревая труба 4.
Эффект охлаждения:
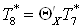 , где , где 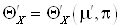 . .
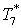 определяется из уравнения для противоточной
трубы 3. определяется из уравнения для противоточной
трубы 3.
Запишем уравнение
теплового баланса с учетом уравнения сохранения энергии
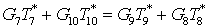 . .
Составим систему
уравнений
 ; ;
 . .
Примем, что 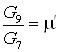 , ,  , , 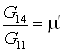 ; и зная, что ; и зная, что 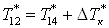 , , 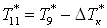 получим получим
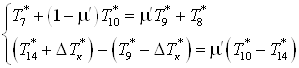 . .
Из второго выражения
системы выразим 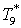 : :
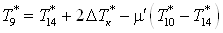 . .
Подставим получившееся
выражение для 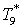 в первое
уравнение системы в первое
уравнение системы
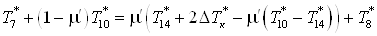 . .
Отсюда
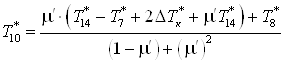 . .
Расходы
 ; ;
 . .
Давление:
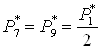 ; ; 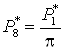 . .
2.6 Эжектор 6.
Запишем уравнение
теплового баланса для эжектора
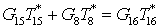 . .
Нам известно, что 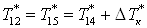 , , 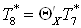 . Если мы разделим каждое
слагаемое уравнения баланса на . Если мы разделим каждое
слагаемое уравнения баланса на 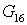 , то
получим , то
получим
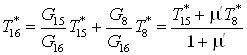 . .
Расходы
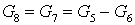 ; ;
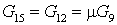 ; ;
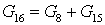 . .
Давление:
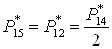 ; ; 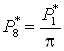 ; ; 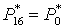 . .
Адиабатный КПД системы,
характеризующий внутреннее совершенство процесса энергоразделения в вихревых
трубах, рассчитывается по зависимости
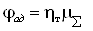 , где , где 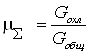 . .
Термический КПД
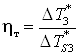 , ,
где 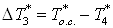 ; ; 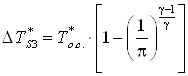 – изоэнтропное охлаждение
газа в процессе адиабатного истечения от давления дополнительно вводимых масс
газа до давления среды, в которую происходит истечение охлажденных масс. – изоэнтропное охлаждение
газа в процессе адиабатного истечения от давления дополнительно вводимых масс
газа до давления среды, в которую происходит истечение охлажденных масс.
Эксергетический КПД будем
определять следующим образом
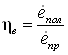 , ,
где  – полезно используемая
эксергия; – полезно используемая
эксергия;  – полная эксергия привода. – полная эксергия привода.
 , ,
где  – эксергия привода для
производства – эксергия привода для
производства 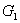 кг/с газа, сжатого до
давления кг/с газа, сжатого до
давления 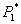 ; ;
 – эксергия привода,
необходимая для сжатия – эксергия привода,
необходимая для сжатия 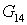 кг/с газа до
давления кг/с газа до
давления 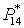 . .
Составим систему
уравнений:
 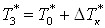 ; ;
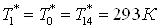 ; ;
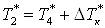 ; ;
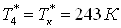 ; ;
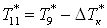 ; ;
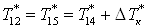 ; ;
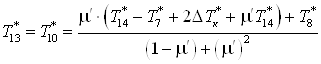 ; ;
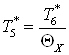 ; ;
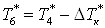 ; ;
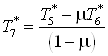 ; ;
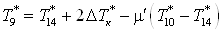 ; ;
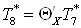 ; ;
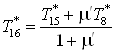 . .
Решая данную систему
уравнений, мы найдем все неизвестные величины.
Приведем пример для
наиболее оптимального режима.
Выбираем 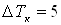
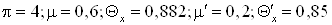
Подставим все в систему:
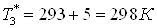 ; ;
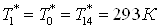 ; ;
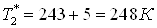 ; ;
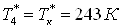 . .
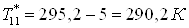 ; ;
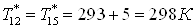
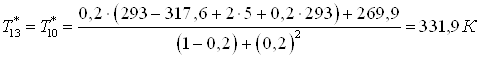
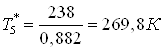
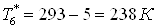
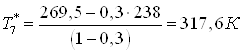
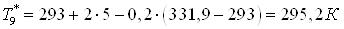 . .
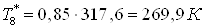
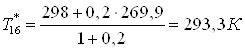 . .
Давления и расходы
представлены в таблицах 2.1 и 2.2:
|
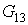
|
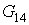
|
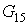
|
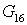
|
|
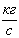
|
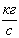
|
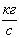
|
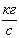
|
| 0,0044 |
0,0044 |
0,0027 |
0,0248 |
Результаты расчетов
сведены в таблицы 2.3, 2.4, 2.5 и представлены на рисунках 2.1, 2.2, 2.3.
Таблица 2.1

|
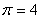
|

|
- |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,86 |
0,88 |
0,9 |
|
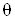
|
- |
0,852 |
0,86 |
0,87 |
0,882 |
0,896 |
0,912 |
0,937 |
0,934 |
0,942 |
|
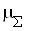
|
- |
0,263 |
0,357 |
0,455 |
0,556 |
0,66 |
0,769 |
0,837 |
0,871 |
0,882 |
|
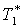
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
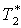
|
К |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
|
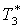
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
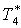
|
К |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
|
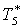
|
К |
279,3 |
276,7 |
273,6 |
269,8 |
265,6 |
260,9 |
254 |
254,8 |
252,7 |
|
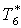
|
К |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
|
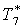
|
К |
297,1 |
302,6 |
309,1 |
317,6 |
330,1 |
352,8 |
352,3 |
390,9 |
384,5 |
|
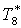
|
К |
252,5 |
257,1 |
262,8 |
269,9 |
280,6 |
299,9 |
299,5 |
332,3 |
326,9 |
|
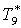
|
К |
298,4 |
297,6 |
296,5 |
295,2 |
293,3 |
289,8 |
289,9 |
283,9 |
284,9 |
|
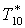
|
К |
315,9 |
320,2 |
325,3 |
331,9 |
341,5 |
359,1 |
358,7 |
388,6 |
383,7 |
|
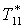
|
К |
293,4 |
292,6 |
291,5 |
290,2 |
288,3 |
284,8 |
284,9 |
278,9 |
279,9 |
|
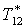
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
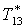
|
К |
315,9 |
320,2 |
325,3 |
331,9 |
341,5 |
359,1 |
358,7 |
388,6 |
383,7 |
|
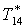
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
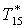
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
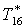
|
К |
290,4 |
291,2 |
292,1 |
293,3 |
295,1 |
298,3 |
298,2 |
303,7 |
302,8 |
|
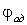
|
% |
13,8 |
16,5 |
19 |
21 |
21,1 |
19,5 |
16,7 |
15 |
14 |
|
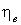
|
% |
5,6 |
6,5 |
7,4 |
8 |
8,16 |
7,80 |
6,80 |
6,1 |
5,1 |
|
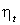
|
% |
29,5 |
36,1 |
41,4 |
45,8 |
49 |
46,8 |
41 |
36,1 |
31,5 |
Таблица 2.2

|

|

|
- |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,86 |
0,88 |
0,9 |
|
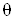
|
- |
0,828 |
0,841 |
0,855 |
0,871 |
0,889 |
0,91 |
0,925 |
0,932 |
0,94 |
|
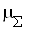
|
- |
0,263 |
0,357 |
0,455 |
0,556 |
0,66 |
0,769 |
0,837 |
0,871 |
0,882 |
|
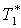
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
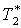
|
К |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
|
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
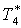
|
К |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
|
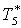
|
К |
287,4 |
282,9 |
278,4 |
273,2 |
267,7 |
261,5 |
257,3 |
255,4 |
253,2 |
|
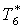
|
К |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
|
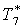
|
К |
308,6 |
312,9 |
318,7 |
326,1 |
337,1 |
355,7 |
375,8 |
395,9 |
389,9 |
|
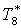
|
К |
268,5 |
272,3 |
277,3 |
283,7 |
293,2 |
309,5 |
326,9 |
344,4 |
339,2 |
|
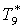
|
К |
295,1 |
294,5 |
293,5 |
292,4 |
290,6 |
287,6 |
284,4 |
281,2 |
282,2 |
|
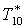
|
К |
332,3 |
335,7 |
340,3 |
346,2 |
354,9 |
369,8 |
385,9 |
401,8 |
397,1 |
|
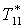
|
К |
290,1 |
289,5 |
288,5 |
287,4 |
285,6 |
282,6 |
279,4 |
276,2 |
277,2 |
|
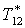
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
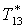
|
К |
332,3 |
335,7 |
340,3 |
346,2 |
354,9 |
369,8 |
385,9 |
401,8 |
397,1 |
|
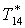
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
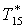
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
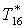
|
К |
293,1 |
293,7 |
294,5 |
295,6 |
297,2 |
299,9 |
302,8 |
305,7 |
304,9 |
|
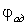
|
% |
12,8 |
15,9 |
18 |
19,3 |
19,6 |
18,3 |
15 |
13 |
12,3 |
|
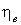
|
% |
4,6 |
5,678 |
6,8 |
7,478 |
7,68 |
7,32 |
6,3 |
5,378 |
4,341 |
|
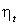
|
% |
26 |
33,5 |
39,6 |
44 |
47 |
45 |
39,6 |
34,7 |
29,7 |
Таблица 2.3

|
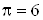
|

|
- |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,86 |
0,88 |
0,9 |
|
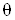
|
- |
0,8 |
0,824 |
0,843 |
0,862 |
0,883 |
0,906 |
0,922 |
0,928 |
0,937 |
|
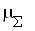
|
- |
0,263 |
0,357 |
0,455 |
0,556 |
0,66 |
0,769 |
0,837 |
0,871 |
0,882 |
|
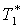
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
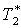
|
К |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
248 |
|
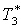
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
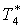
|
К |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
243 |
|
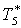
|
К |
287,4 |
282,9 |
278,4 |
273,2 |
267,7 |
261,5 |
257,3 |
255,4 |
253,2 |
|
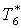
|
К |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
238 |
|
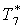
|
К |
308,6 |
312,9 |
318,7 |
326,1 |
337,1 |
355,7 |
375,8 |
395,9 |
389,9 |
|
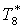
|
К |
290,1 |
294,2 |
299,6 |
306,6 |
316,8 |
334,4 |
353,3 |
372,1 |
366,5 |
|
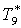
|
К |
290 |
289,2 |
288,2 |
286,9 |
284,9 |
281,7 |
278,2 |
274,6 |
275,7 |
|
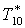
|
К |
357,9 |
361,8 |
366,9 |
373,4 |
383 |
399,4 |
417,2 |
434,8 |
429,6 |
|
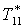
|
К |
285 |
284,2 |
283,2 |
281,9 |
279,9 |
276,7 |
273,2 |
269,6 |
270,7 |
|
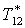
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
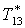
|
К |
357,9 |
361,8 |
366,9 |
373,4 |
383 |
399,4 |
417,2 |
434,8 |
429,6 |
|
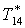
|
К |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
293 |
|
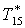
|
К |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
298 |
|
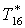
|
К |
296,7 |
297,4 |
298,3 |
299,4 |
301,1 |
304,1 |
307,2 |
310,4 |
309,4 |
|
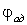
|
% |
8,39 |
10,9 |
14,1 |
15,5 |
15,7 |
15,1 |
13,4 |
12 |
11,4 |
|
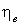
|
% |
3,7 |
5 |
6,3 |
7 |
7,3 |
7 |
6 |
4,9 |
4 |
|
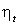
|
% |
23,6 |
30,8 |
36,7 |
42,3 |
45,1 |
43,3 |
36,7 |
32,1 |
27,5 |
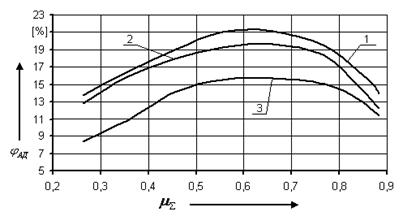
Рис.2.1 – 1 – Зависимость
адиабатного КПД схемы от суммарной доли
охлажденного потока при 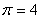
2 – Зависимость
адиабатного КПД схемы от суммарной доли
охлажденного потока при 
3 –Зависимость
адиабатного КПД схемы от суммарной доли охлажденного потока при 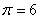
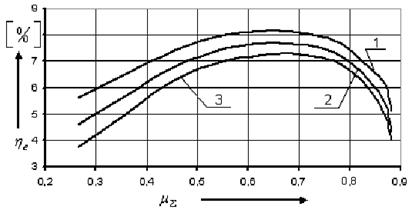
Рис.2.2 – 1 – Зависимость
эксергетического КПД от суммарной доли охлажденного потока при 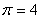
2 – Зависимость
эксергетического КПД от суммарной доли охлажденного потока при 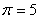
3 – Зависимость
эксергетического КПД от суммарной доли охлажденного потока при 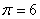
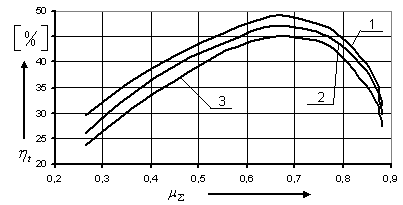
Рис.2.3 – 1 – Зависимость
термического КПД от суммарной доли охлажденного потока 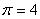
2 – Зависимость
термического КПД от суммарной доли
охлажденного потока при 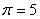
3 – Зависимость
термического КПД от суммарной доли
охлажденного потока при 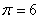
3 Расчет потребного количества сжатого воздуха
Расчетная
холодопроизводительность схемы
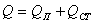 , ,
где 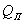 - потребная
холодопроизводительность. По техническому заданию - потребная
холодопроизводительность. По техническому заданию 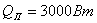 , ,
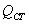 - потери тепла через
изоляцию стенок термокамеры - потери тепла через
изоляцию стенок термокамеры
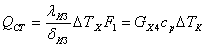 , , 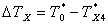 , ,
где 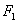 - поверхность теплообмена - поверхность теплообмена 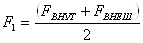 ; ;
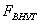 - внутренняя поверхность
термокамеры. - внутренняя поверхность
термокамеры.
Потребный объем
термокамеры
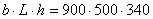
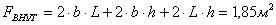
Толщина изоляции: 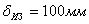 . .
Внешняя поверхность
камеры: 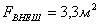 . .
Расчетная поверхность
теплообмена: 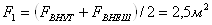 . .
Изоляция: пенопласт марки
Ф-Ф.
Коэффициент
теплопроводности изоляции: 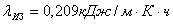
Расчет холодного воздуха
для охлаждения стенок термокамеры
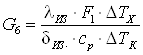
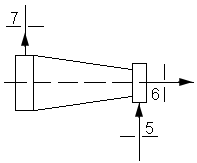
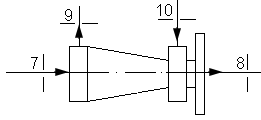
4 Расчет эжектора.
Эжектор 6
Исходные данные:
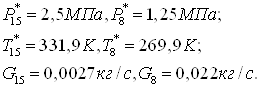
Где  - давление, температура и
расход эжектирующего (активного) газа; - давление, температура и
расход эжектирующего (активного) газа;
 - давление, температура и расход
эжектируемого (пассивного) газа; - давление, температура и расход
эжектируемого (пассивного) газа;
Статическое давление на
выходе из эжектора принимаем равным 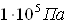
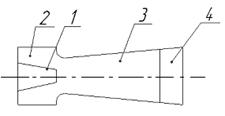
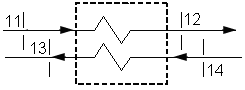
1-
сопло
эжектирующего газа
2-
сопло
эжектируемого газа
3-
камера смешения
4-
диффузор
Рис. 4.1 – Расчетная
схема эжектора
Считая ср=const определяем коэффициент эжекции
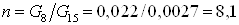 . .
Определяем безразмерные
параметры:
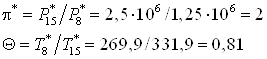
Область реально возможных
режимов. Найдем критическую величину  -
предельно возможное значение -
предельно возможное значение 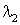 , при
котором в сечении запирания скорость эжектируемого газа, то есть , при
котором в сечении запирания скорость эжектируемого газа, то есть 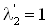 . Так как отношение . Так как отношение 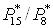 - невелико, то
воспользуемся уравнением, полученным в предположении равенства статических
давлений в сечении запирания: - невелико, то
воспользуемся уравнением, полученным в предположении равенства статических
давлений в сечении запирания:
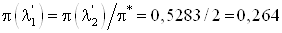
Откуда следует при 
Определяем 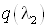 из уравнения из уравнения
 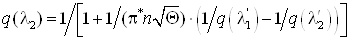
Подставляя численные
значения, получим 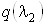 =0,987. =0,987.
Этому значению
соответствует предельно возможное значение λ2=0,90.
Из уравнения импульсов,
которое принимает вид
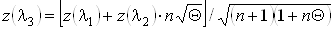 , ,
Определим значение 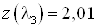 , то есть , то есть 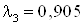 при при 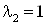 или или 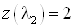
Таким образом, предельно
возможное значение 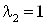 оказывается
выше, чем определено из рассмотрения потоков сечении запирания (λ2=0,90). оказывается
выше, чем определено из рассмотрения потоков сечении запирания (λ2=0,90).
Принимаем 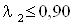 . .
Для расчета эжектора
зададимся рядом значений коэффициента скорости λ2 . Задаемся
несколькими значениями 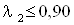 и проводим
расчет по изложенному выше методу. и проводим
расчет по изложенному выше методу.
Данные расчета и
результаты заносим в таблицу 2.4.
Таблица 2.4
| Величина |
Размерность |
Значение величин при λ2 равном
|
| 0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
|
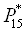
|
МПа |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
|
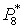
|
МПа |
1,25 |
1,25 |
1,25 |
1,25 |
1,25 |
|
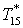
|
К |
331,9 |
331,9 |
331,9 |
331,9 |
331,9 |
|
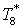
|
К |
269,9 |
269,9 |
269,9 |
269,9 |
269,9 |
|
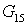
|
кг/с |
0,0027 |
0,0027 |
0,0027 |
0,0027 |
0,0027 |
|
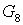
|
кг/с |
0,022 |
0,022 |
0,022 |
0,022 |
0,022 |
|
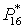
|
МПа |
5 |
5 |
5 |
5 |
5 |
|
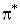
|
- |
2 |
2 |
2 |
2 |
2 |
|
n
|
- |
8,1 |
8,1 |
8,1 |
8,1 |
8,1 |
| Θ |
- |
0,81 |
0,81 |
0,81 |
0,81 |
0,81 |
|
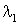
|
- |
1 |
1 |
1 |
1 |
1 |
|
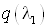
|
- |
1 |
1 |
1 |
1 |
1 |
|
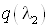
|
- |
1,012 |
1,008 |
1,006 |
1,003 |
1,002 |
|
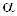
|
- |
0,0694 |
0,0692 |
0,0689 |
0,688 |
0,0687 |
|
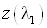
|
- |
1 |
1 |
1 |
1 |
1 |
|
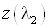
|
- |
2,19 |
2,13 |
2,08 |
2,05 |
2,03 |
|
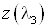
|
- |
2,16 |
2,11 |
2,07 |
2,04 |
2,02 |
|
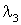
|
- |
0,672 |
0,719 |
0,768 |
0,819 |
0,868 |
5.1 Теплообменные
аппараты 5
В теплообменник 5а от
источника сжатого воздуха подводится энергия  и
от охлаждаемого объекта 2 энергия и
от охлаждаемого объекта 2 энергия  ,
которые рассчитываются: ,
которые рассчитываются:
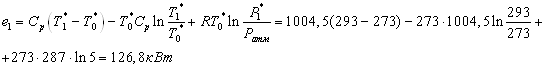
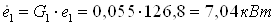
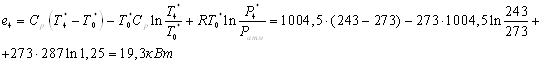
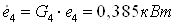
От теплообменника 5а
отводится энергия  и и  : :
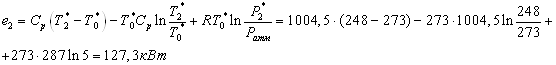
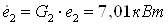
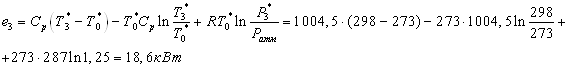
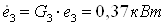
В теплообменник 5б от
источника сжатого воздуха подводится энергия  и
от подогреваемого объекта 1 энергия и
от подогреваемого объекта 1 энергия  ,
которые рассчитываются: ,
которые рассчитываются:
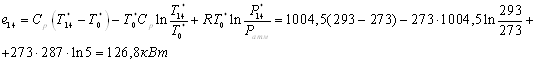
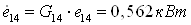
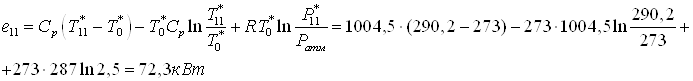
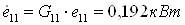
От теплообменника 5б
отводится энергия  и и  : :
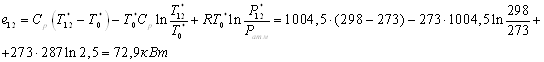
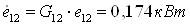
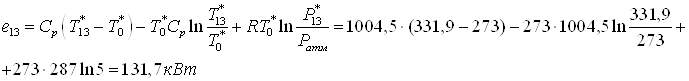
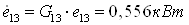
5.2 Противоточная
вихревая труба 3.
К противоточной вихревой
трубе подводится энергия  , а
отводится с холодного конца , а
отводится с холодного конца  и с
горячего и с
горячего  : :
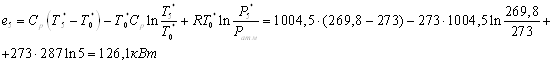 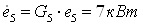
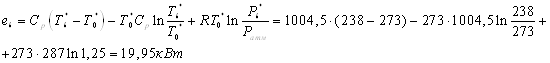 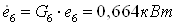
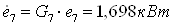
5.3 Охлаждаемый объект 2.
К охлаждаемому объекту с
холодного конца противоточной вихревой трубы 3 подводится  , а отводится , а отводится  , рассчитанные ранее. , рассчитанные ранее.
5.4 Подогреваемый объект
1.
К подогреваемому объекту
с горячего конца двухконтурной вихревой трубы 4 подводится  , а отводится , а отводится  (рассчитана ранее): (рассчитана ранее):
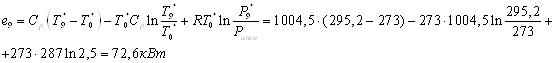 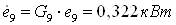
5.5 Двухконтурная
вихревая труба 4.
К двухконтурной вихревой
трубе подводится от противоточной вихревой трубы 3 энергия  (рассчитана ранее) и от
теплообменника (рассчитана ранее) и от
теплообменника  , а отводится с горячего
конца трубы , а отводится с горячего
конца трубы  (рассчитана ранее) и с
холодного конца (рассчитана ранее) и с
холодного конца  : :
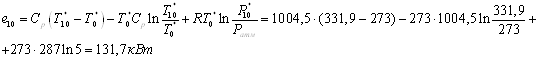 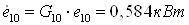
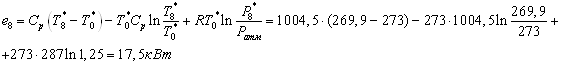 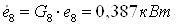
5.6 Эжектор 6.
К эжектору подводится с
холодного конца двухконтурной вихревой трубы энергия  (рассчитана ранее) и от
теплообменника (рассчитана ранее) и от
теплообменника 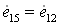 (рассчитана
ранее), а отводится (рассчитана
ранее), а отводится  : :
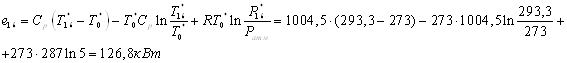 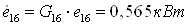
По известному расходу и
параметрам сжатого воздуха найдем минимальный диаметр камеры энергоразделения
противоточной вихревой трубы, предварительно определив площадь проходного
сечения сопла завихрителя:
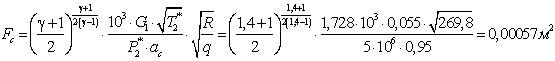
 - коэффициент расхода сопла. - коэффициент расхода сопла.
Размеры проходного
сечения прямоугольного сопла:
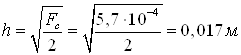
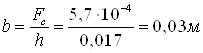
Относительный диаметр
отверстия диафрагмы:
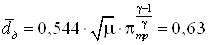
Диаметр вихревой трубы:
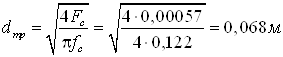 где где 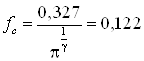
Диаметр диафрагмы:
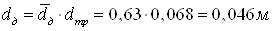
Длина трубы выбирается:
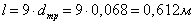
Заключение
В процессе выполнения
курсовой работы в соответствии с заданием варианта ВХНА № 1 осуществлен
тепловой расчет схемы в целом и произведен термодинамический расчет вихревой
трубы в характерных сечениях. Оптимальный режим достигается при относительной
доле холодного потока в двухконтурной вихревой трубе 4  ; в противоточной вихревой
трубе 3 ; в противоточной вихревой
трубе 3 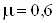 при степени расширения
потока при степени расширения
потока 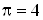 . .
На эксергетической
диаграмме видно, что наибольшие потери эксергии возникают в вихревых трубах.
Рассчитана геометрия
противоточной вихревой трубы: площадь проходного сечения сопла завихрителя 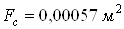 ; диаметр вихревой трубы ; диаметр вихревой трубы 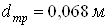 ; диаметр диафрагмы ; диаметр диафрагмы 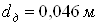 ; длина трубы ; длина трубы 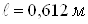 . .
Список
используемой литературы
1.
Пиралишвили,
Ш.А. Термодинамика
технических устройств. Учебное пособие/[Текст] Ш.А. Пиралишвили, М.Н. Сергеев.
- Рыбинск, РГАТА, 2001
2.
Пиралишвили,
Ш.А. Вихревой
эффект. Эксперимент, теория, технические решения/[Текст] Ш.А. Пиралишвили, В.М.
Поляев, М.Н. Сергеев. - М.: УНПЦ Энергомаш, 2000.- 415с.
3.
Абрамович,
Г.Н. Прикладная
газовая динамика/[Текст] Г.Н. Абрамович.- М.: Наука, 1991.-600с.
|







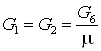 ;
;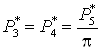

 ;
; .
.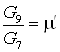 ,
,  ,
, 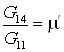 ; и зная, что
; и зная, что 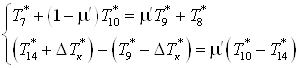 .
.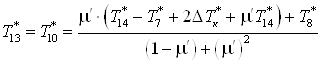 .
.
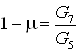 , а
, а 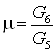 . Тогда уравнение баланса
примет вид
. Тогда уравнение баланса
примет вид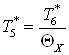 .
.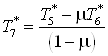 .
.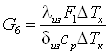 ;
;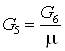 ;
;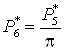 ;
; 
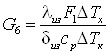 ;
;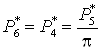 .
.
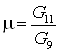 .
.
 ;
; .
.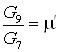 ,
,  ,
, 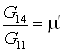 ; и зная, что
; и зная, что 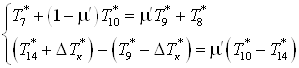 .
.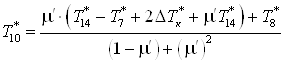 .
.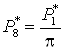 .
.
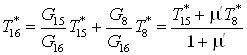 .
.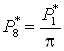 ;
; 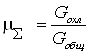 .
.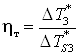 ,
,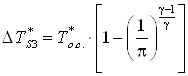 – изоэнтропное охлаждение
газа в процессе адиабатного истечения от давления дополнительно вводимых масс
газа до давления среды, в которую происходит истечение охлажденных масс.
– изоэнтропное охлаждение
газа в процессе адиабатного истечения от давления дополнительно вводимых масс
газа до давления среды, в которую происходит истечение охлажденных масс.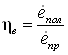 ,
,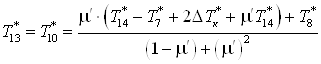 ;
;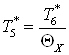 ;
;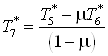 ;
;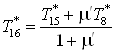 .
.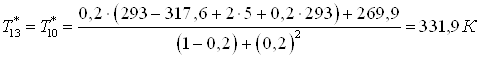
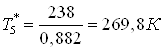
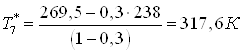
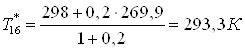 .
.


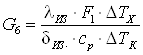
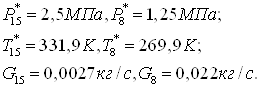

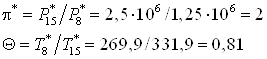
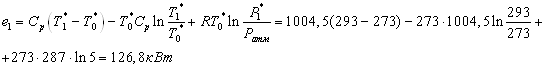
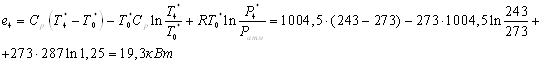
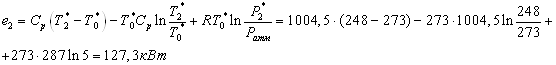
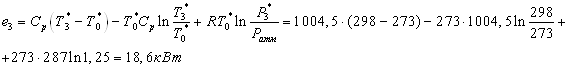
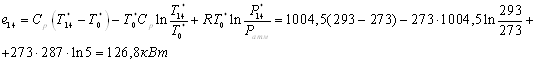
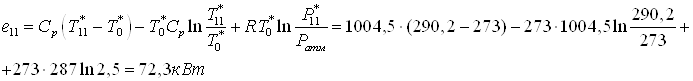
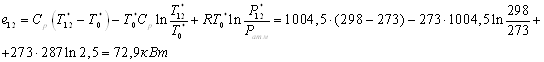
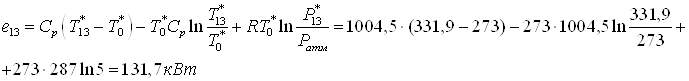
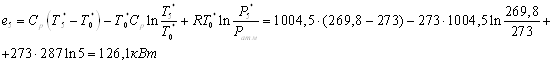
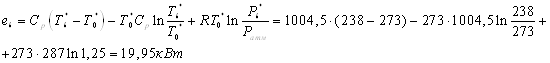
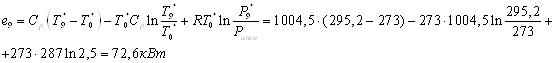
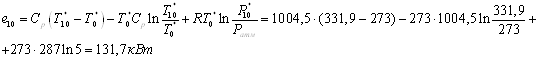
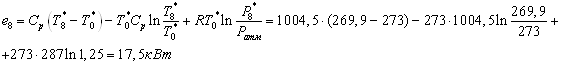
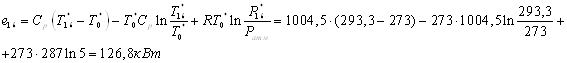
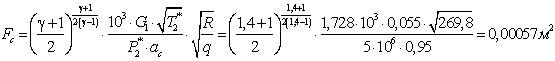
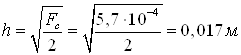
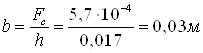
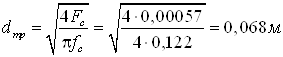 где
где