Промышленность производство : Курсовая работа: Привод цепного конвейера
Курсовая работа: Привод цепного конвейера
1. Энергетический
и кинематический расчёт привода
1.1 Исходные
данные:
Ft- окружная
сила на звездочке цепного конвейера, кН; 1,00
V - скорость
движения цепи, м/с; 0,75
Z – число
зубьев звездочки; 9
P – шаг
тяговых звездочек, мм; 100
1.2 Выбор
электродвигателя.
1.2.1
Определение потребляемой мощности привода
Рвых.
= FtּV, (1.1)
где Рвых.-
потребляемая мощность привода, кВт
Рвых
= 1 ּ 0,75 м/с = 0,75 кВт
1.2.2
Определение потребляемой мощности электродвигателя
Рэ
= Рвых / ףоб, (1.2)
где Рэ
- потребляемая мощность электродвигателя;
ףоб – общий КПД привода,
определяемый как произведение КПД отдельных передач и муфт.
ףоб= ףц.п ּ ףк.п ּ
ףм, ּ ףм (1.3)
где ףц.п – КПД цилиндрической
передачи, ףц.п=0,96 – 0,98;
ףц.п – КПД конической
передачи, ףц.п=0,95 – 0,97;
ףм – КПД муфты, ףм=0,98.
ףоб= 0,97•0,96•0,982 =
0,89
Рэ
=0,75/0,89=0,84 кВт
1.2.3
Определение предполагаемой частоты вращения вала электродвигателя
nэ=
nвּ u1ּu2ּ …(1.4)
где u1,
u2 - рекомендуемые значения передаточных чисел передач привода;
nв -
частота вращения приводного вала, мин.-1
nэ
предполагаемая частота вращения вала электродвигателя, мин-1
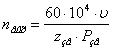 , (1.5) , (1.5)
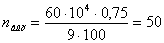 мин-1 мин-1
Принимаем
значения передаточных чисел:
Uб=
2,5- 5 Uт=2-5
nэ=50×4,5×4=900 мин.-1
По найденным
значениям Рэ и nэ выбираем электродвигатель:
Электродвигатель
АИР 90LB8 ТУ 16-525.564-84
Pэ
= 1,1 кВт,nэ = 695 об./мин.
1.3 Определение
общего передаточного отношения привода и разбивка его по ступеням
После выбора
электродвигателя определяем общее передаточное число привода:
Uобщ=
nэ/ nв (1.6)
где nэ -
номинальная частота вращения вала выбранного электродвигателя, мин.-1
Uобщ=
695/50= 13,9
Uред=
Uобщ (1.7)
Uред=
13,9
Далее
производим распределение передаточного числа редуктора между его ступенями.
 , (1.8) , (1.8)
где Uт
передаточное число тихоходной ступени.
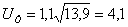
Из
стандартного ряда чисел принимаем Uт=4 по СТСЭВ 229-75
Uб=Uред/Uт,
(1.9)
где Uб
передаточное число быстроходной ступени
Uб=13,9/4=3,48
Из
стандартного ряда чисел принимаем Uб=3,55 по СТСЭВ 229-75
1.4 Определение
мощности на валах, частоты вращения валов и крутящих моментов на валах
Мощности на
валах определяют через мощность электродвигателя
P1
= Pэ ּ
ףм, (1.10)
где P1
мощность на первом валу, кВт;
ףм – КПД муфты
P1
= 1,1×0,98=1,08 кВт
P2
= P1 ּ
ףк.п., (1.11)
где P2
мощность на втором валу, кВт;
ףк.п. – КПД конической
передачи
P2
= 1,08×0,96=1,05 кВт
P3
= P2 ּ
ףц.п., (1.12)
где P3
мощность на третьем валу, кВт;
ףц.п. – КПД цилиндрической
передачи
P3
= 1,05·0,97=1 кВт
Частоты
вращения валов могут быть определены через частоту вращения вала
электродвигателя.
n1
= nэ = 695 мин-1 (1.13)
ni=ni-1/Ui,
(1.14)
где ni,
ni-1 – частота вращения соответственно i и i-1 валов, мин-1
n2
= n1 /uб, (1.15)
где uб
передаточное число быстроходной ступени.
n2
= 695/3,55=195,77 мин-1
n3
= n2 /uт, (1.16)
где uт
передаточное число тихоходной ступени.
n3
= 195,77/4=48,94 мин-1
Крутящие
моменты на валах определяются по формуле:
Ti
=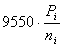 , Н ּ м(1.17) , Н ּ м(1.17)
где Ti
- крутящий момент на i-ом валу, Н • м;
Рi
- мощность на i-ом валу, кВт;
n - частота
вращения i-ого вала, мин-1
T1
= 9550 ּ P1/n1
= 9550 ּ1,08/695 = 14,84 Н ּ м (1.18)
T2
= 9550 ּ P2/n2
= 9550 ּ 1,05/195,77 =51,22 Н ּ м (1.19)
T3
= 9550 ּ P3/n3
= 9550 ּ 1/48,94 = 195,14 Н ּ м (1.20)
Результаты
произведенных расчетов, в соответствии с таблицей 1.1, являются исходными
данными для последующих расчетов передач.
Таблица 1.
| Валы |
Мощности на валах, кВт |
Частоты вращения валов,
мин-1
|
Крутящие моменты на
валах, Н ּ м |
Передаточные числа
передач |
|
I
II
III
|
1,08
1,05
1
|
695
195,77
48,94
|
14,84
51,22
195,14
|
Uб=3,55
Uт=4
|
2. Расчёт
тихоходной ступени закрытой косозубой цилиндрической передачи
2.1 Исходные
данные
Крутящий
момент на шестерне Т1=51,22 Н·м;
Крутящий
момент на колесе Т2=195,14 Н·м;
Частота
вращения шестерни n1 =195,77 мин-1;
Частота
вращения колеса n2 =48,94 мин-1;
Передаточное
число U = 4;
Срок службы
передачи L = 5 лет;
Коэффициент
суточного использования КС =0,29;
Коэффициент
годового использования КГ =0,8.
2.2 Выбор
материала и термической обработки колес
Шестерня: сталь 40Х, Термообработка
- улучшение и закалка ТВЧ,
твёрдость
45-50 HRC.
Колесо: сталь
40Х, Термообработка – улучшение и закалка ТВЧ, твёрдость 45-50 HRC.
2.3
Определение
допускаемых напряжений
2.3.1 Определение
срока службы передачи
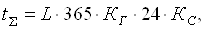 (2.1) (2.1)
где tΣ
срок службы передачи, час.
tΣ=5·365·0,8·24·0,29=10161
час.
2.3.2 Определяем
допускаемые напряжения на контактную прочность
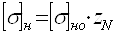 , (2.2) , (2.2)
где 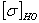 - базовое
допускаемое напряжение, Мпа; - базовое
допускаемое напряжение, Мпа;
zN
коэффициент долговечности.
Базовые
допускаемые напряжения [σ]но определяется по формуле:
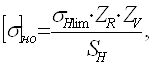 (2.3) (2.3)
где σHlim
- длительный предел контактной выносливости, МПа;
ZR
- коэффициент, учитывающий шероховатость сопряженных поверхностей, ZR=
1;
ZV
- коэффициент, учитывающий влияние скорости,
ZV
= 1;
SH
- коэффициент запаса прочности, SH =1,3 – при однородной структуре
материала;
SH
=1,3 – при поверхностных упрочнениях;
Коэффициент
долговечности ZN определяется по формуле:
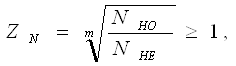 (2.4) (2.4)
где NHO -
базовое число циклов нагружения;
NHE -
эквивалентное число циклов нагружения;
m - показатель степени кривой
усталости поверхностных слоев зубьев, m=6.
Базовое число
циклов нагружения NHO принимается равным:
 (2.5) (2.5)
Если NНО
получится больше 12·107, то принимают 12·107.
Когда
твёрдость задана в HRC, то
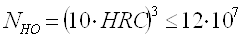 (2.6) (2.6)
Эквивалентное
число циклов нагружения NHE определяется по зависимости:
NHE
=60 × n × tS Σ(Ti/TH)m/2·ti/t=
=60
× n × tS (a1b13
+ a2b23+…+ aibi3),
(2,7)
где ai,bi
коэффициенты с графика нагрузки (рис.2.1)
В случае
получения NHE> NHО, ZN=1.
| Шестерня |
Колесо
|
|
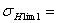 17HRC+200=17·47.5+200= 17HRC+200=17·47.5+200=
=1007.5 МПа
ZR=1,
ZV=1, SH=1.3
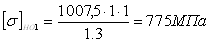
NHE1=60·195,77·10161·(13×0,15+
+0,53×0,85) = 3,06·107
NHО1=(47,5·10)3=10,7·107<12·107
|
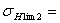 17HRC+200=17·47.5+200= 17HRC+200=17·47.5+200=
=1007.5 МПа
ZV=1,
SH=1,3, ZR=1
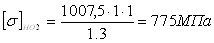
NHE2=60·48,94·10161·(13×0,15+0,53×0,85)=
=0,75·107
NHО2=(47,5·10)3=10,7·107<12·107
|
|
NHE< NHО
условие выполняется
|
|
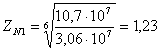
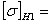 775·1,23=953,25МПа 775·1,23=953,25МПа
|

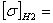 775·1,56=1209 МПа 775·1,56=1209 МПа
|
|
|
|
За расчётное
принимаем наименьшее напряжение:
[σ]HP=953,25МПа
расчётное допускаемое напряжение.
2.3.3 Определение допускаемых
напряжений при расчете зубьев на изгиб
Допускаемое
напряжение на изгиб [σ]F, МПа определяется по формуле:
[σ]F
= [σ]FО × YA× YN, (2.8)
где [σ]FО
- базовые допускаемые напряжения изгиба при нереверсивной нагрузке, МПа;
YA
- коэффициент,
вводимый при двустороннем приложении нагрузки: YA=1;
YN-–коэффициент
долговечности.
Базовые
допускаемые напряжения на изгиб [σ]FО, определяются по формуле:
[σ]FО
= (σFim×YR×YX×Yб)/SF,
(2.9)
где σFim
- предел выносливости, определяемый на зубьях при нулевом цикле, МПа;
YR -
коэффициент, учитывающий шероховатость поверхности; при шлифовании
YR =1;
YX
коэффициент размеров, YX =1;
Yб -
коэффициент, учитывающий чувствительность материала и концентрации напряжений,
Yб =1;
SF
коэффициент запаса прочности, SF=1,7.
Коэффициент
долговечности YN определяют как:
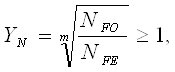 (2.11) (2.11)
где NFO
- базовое число циклов нагружения, NFO =4×106;
NFЕ
- эквивалентное
число циклов нагружения;
m - показатель степени кривой
выносливости; m=6 – улучшение, нормализация, т=9 –объемная и
поверхностная закалка;
Эквивалентное
число циклов нагружения NFЕ определяются по формуле:
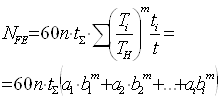 (2.12) (2.12)
При NFE>NFO
коэффициент долговечности YN=1.
| Шестерня |
Колесо |
|
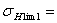 500-600МПа=550 МПа 500-600МПа=550 МПа
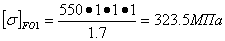
NFE1=60·195,77·10161·(19·0,15+
+0,59·0,85)=
18,1·107
NFE1> NFO
=> YN=1
|
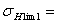 500-600МПа=550 МПа 500-600МПа=550 МПа
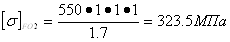
NFE2=60·48,94·10161·(19·0,15+0,59·0,85)=
=4,55·107
NFE2> NFO
=> YN=1
|
|
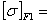 323,5·1·1=323,5МПа 323,5·1·1=323,5МПа
|
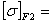 323,5·1·1=323,5МПа 323,5·1·1=323,5МПа
|
|
|
|
2.3.4 Определение
межосевого расстояния
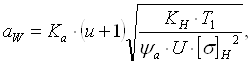 (2,13) (2,13)
где aw-
межосевое расстояние, мм;
Ka
- вспомогательный коэффициент, Ka = 450;
КН
коэффициент нагрузки;
ψa -
коэффициент ширины.
Коэффициент
ширины принимаем равным ψa=0,25;
Коэффициент
нагрузки принимаем равным KH=1,4.

Из
нормального ряда чисел принимаем 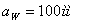
2.3.5
Определение модуля передачи
Для зубчатых
колес при твердости зубьев 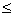 350 HB модуль назначают: 350 HB модуль назначают:
m =
(0,01…0,02)аW, (2,14)
а при
твёрдости >45 HRC
mn
= (0,016-0,0315) aw (2,15)
mn
= (0,016-0,0315)×100
mn
= 1,6 – 3,15
Стандартное
значение модуля m=2 (ГОСТ 9563-80).
2.3.5 Определение
суммарного числа зубьев для косозубой передачи
zΣ
= 2×aw/mn, (2,16)
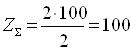
2.3.7 Определение числа зубьев
шестерни
z1
= zΣ/(u+1) (2,17)
z1
= 100/5=20
Z1>Zmin,
(2,18)
где Zmin=17
для прямозубых передач.
Условие
выполняется.
2.3.8 Определение
числа зубьев колеса
z2
= zΣ- z1 (2,19)
z2=
100-20 =80
2.3.9 Определение
геометрических размеров колес и шестерён
Делительные
диаметры:
d=mn
×z
d1=2×20=40 мм d2=2×80=160 мм
Диаметры
вершин зубьев:
da =
d + 2·mn (2,20)
da1
= d1 + 2·mn = 40 + 2·2 = 44 мм;
da2
= d2 + 2·mn = 160 + 4 = 164 мм;
Диаметры
впадин зубьев:
df =
d – 2.5·mn (2,21)
df1 =
d1 – 2.5·mn = 40 – 2,5·2 = 35 мм;
df2 =
d2 – 2.5·mn = 160 – 2,5·2 = 155 мм;
Ширина
колеса:
b2 =
ψa · aW (2,22)
b2 =
ψa · aW = 0.25·100 = 25 мм
Ширина
шестерни:
b1 =
b2 + 5мм (2,23)
b1 =
b2 + 5 = 25 + 5 = 30 мм
2.3.10
Определение усилий в зацеплении
Окружное
усилие:
Ft
= (2×T) / d, (2,24)
где Ft-
окружное усилие, кН;
T - крутящий
момент на зубчатом колесе, Н • м;
d - делительный диаметр
колеса, мм;
Ft =
(2×51,22)/40 = 2,56кН
Радиальное
усилие:
Fr=Ft• tgαw (2.25)
где aw
- угол зацепления, aw =20°.
Fr=2,56•tg20 = 0,93 кН
2.3.11 Проверка
зубьев колес по напряжениям изгиба
Для этого
производят оценку изгибной прочности, т.е. находят отношения:
[σ]F1/YF1
и [σ]F2/ YF2 (2,26)
Коэффициенты
формы зубьв YF1 и YF2 определяются по эквивалентному
числу зубьев шестерни и колеса:
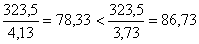
YF1=4,13
YF2=3,73
Расчёт
ведётся по шестерне.
Напряжения
изгиба определяются по формуле:
σF
= (2×103× YF×KFα× KFβ ·KFV×T)/(m2×Z×b)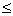 [σ]F, (2,27) [σ]F, (2,27)
где σF
- рабочее напряжение изгиба, МПа;
KFα
коэффициент распределения нагрузки между зубьями, зависящими от окружной
скорости колеса;
KFβ
- коэффициент концентрации нагрузки;
KFV
-коэффициент динамичности нагрузки;
Коэффициент
концентрации нагрузки KFβ назначают в зависимости от
коэффициента ширины:
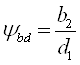 (2,28) (2,28)
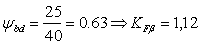
Для
определения коэффициента динамичности нагрузки KFV предварительно
необходимо определить окружную скорость колеса:
V= (π×d×n)/(6×104), (2,28)
где V - скорость
колеса, м/с;
d - делительный диаметр, мм;
n - частота вращения колеса,
мин-1
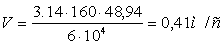
По скорости
назначаем степень точности колеса – 8 степень точности и коэффициент
динамичности KFV = 1,04
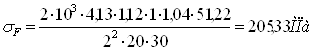
σF1
=205,3МПа < [σ]F1 = 323,5МПа
Прочность
зубьев на изгиб обеспечена.
2.3.12
Проверка зубьев колес на контактную прочность
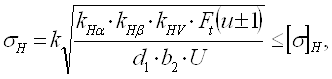 (2,29) (2,29)
где σH-контактные
напряжения, МПа;
К -
вспомогательный коэффициент, К =428 – для прямозубой передачи;
KHα-
коэффициент распределения нагрузки между зубьями, КHα = 1;
KHβ
- коэффициент концентрации нагрузки, KHβ = 1,08;
KHV-
коэффициент динамичности нагрузки, KHV=1,03;
Ft-
окружное усилие, Н;
d1-
делительный диаметр шестерни, мм;
b2-
ширина колеса, мм.

σH
= 801,5 МПа < [σ]H = 953, 25 МПа
Прочность
зубьев обеспечена.
3. Расчёт
прямозубой конической передачи
3.1
Исходные данные
Крутящий
момент на шестерне T1 = 14,84 Hм;
Крутящий
момент на колесе T2 = 51,22 Hм;
Частота
вращения шестерни n1 =695 мин-1;
Частота
вращения колеса n2 = 195,77 мин-1;
Передаточное
число u = 3,55;
Срок службы
передачи L = 5лет;
Коэффициент
суточного использования Kc = 0,29;
Коэффициент
годового использования Kr = 0,8.
3.2 Выбор
материала и термообработки
Шестерня:
Сталь 40Х. Термообработка: улучшение и закалка ТВЧ. Твёрдость 45-50HRCэ.
Колесо: Сталь
40Х. Термообработка: улучшение и закалка ТВЧ. Твёрдость 45-50HRCэ.
3.3 Определение
допускаемых напряжений
3.3.1 Определение срока службы
передачи
tΣ
= 10161 часов – определено ранее.
3.3.2
Определение допускаемых напряжений на контактную прочность
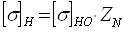 , (3,1) , (3,1)
где 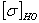 - базовое
допускаемое напряжение, МПа; - базовое
допускаемое напряжение, МПа;
ZN
коэффициент долговечности
Определяем
базовые допускаемые напряжения:
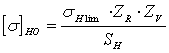 (3,2) (3,2)
ZR=1
(т.к. проводится шлифование закалённой шестерни);
ZV=1
(проектный расчёт);
SH=1,3
(поверхностное упрочнение).
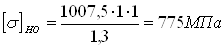
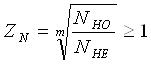 (3.3) (3.3)
m
= 6; 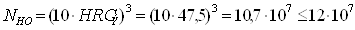
NHE=60·n·tΣ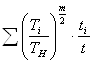 = =
=60·n·tΣ (a1b13+a2b23+…+
aibi3) (3.4)
| Шестерня |
Колесо |
|
NHE1=60·695·10161·(13·0,15+
+0,53·0,85)=10,9·107
NHE1> NHО1=>ZN1=1
|
NHE2=60·195,77·10161·(13·0,15+
+0,53·0,85)=3,06·107
NHE2< NHО

|
|
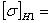 775·1=775МПа 775·1=775МПа
|
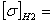 775·1,23=953,25 МПа 775·1,23=953,25 МПа
|
|
|
|
За расчётное
принимаем 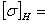 775МПа 775МПа
3.3.3
Определение допускаемых напряжений при расчёте зубьев на изгиб
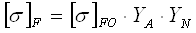 (3,5) (3,5)
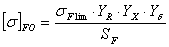 (3,6) (3,6)
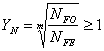 (3,7) (3,7)
NFO=4·106;
m=9
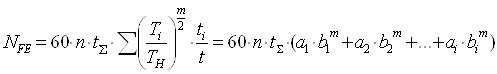 (3.8) (3.8)
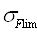 =550МПа, YR=1,YX=1,Yδ=1,SF=1,7 =550МПа, YR=1,YX=1,Yδ=1,SF=1,7
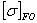 =550·1·1·1/1,7=323,5МПа =550·1·1·1/1,7=323,5МПа
|
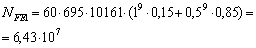
NFE1>NFО=>YN1=1
|
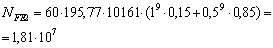
NFE2>NFО=>YN2=1
|
YA=1
передача нереверсивная

3.3.4 Определение
диаметра внешней делительной окружности колеса
de2=
1650·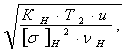 (3,9) (3,9)
где de2
- диаметр внешней делительной окружности колеса, мм;
KH
- коэффициент
нагрузки, KH =1,5;
Т2
- крутящий
момент на колесе, Н • м;
[σ]H
- допускаемые напряжения на контактную прочность, МПа;
VH - коэффициент понижения контактной
прочности конической передачи, VH =0,85.
de2
= 1650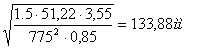
Назначаем de2ст
= 140 мм.
3.3.5 Определение
числа зубьев шестерни
Определяем
делительный диаметр шестерни:
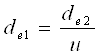 (3.10) (3.10)
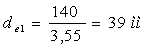
По
делительному диаметру назначаем число зубьев шестерни Z1`=Z=17 т.к.
Н1 и Н2 >45 HRCЭ.
3.3.6
Определение числа зубьев колеса
Z2
=Z1×u (3.11)
Z2
= 17·3,55=60
3.3.7 Определение
торцевого модуля
mte
= de2ст./Z2 (3.12)
mte
= 140/60=2,33 мм
Стандартное
значение торцевого модуля mte = 2,25мм (ГОСТ 9563-80)
3.3.8Уточнение
диаметра делительной окружности колеса
de2
= mte ×Z2 (3,13)
de2
= 2,25·60=135 мм
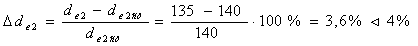
Фактическое
передаточное число: Uфак=60/17=3,53
3.3.9 Определение
внешнего конусного расстояния
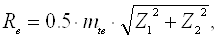 (3,14) (3,14)
где z 1и
z2 - фактические числа зубьев шестерни и колеса.
Re
= 0.5×2,25×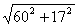 = 70,16мм = 70,16мм
3.3.10 Определение ширины колес
b = kbe×Rbe, (3,15)
где kbe
коэффициент ширины, kbe = 0,285
b = 0,285·70,16=19,99
берём в=20
мм
3.3.11 Определение
углов наклона образующих делительных конусов
δ2
= arctg Uфакт. (3,16)
δ1=
900- δ2 (3,17)
δ2
= arctg 3,53 = 74,20
δ1=
900-74,20 = 15,80
3.3.12
Определение диаметров колес
Делительные
диаметры:
de1 =
mte × z1 (3,18)
de2
= mte × z2 (3,19)
de1
=2,25·17=38,3мм
de2
= 2,25·60=135мм
Внешние диаметры:
dae1
= de1+2(1+x1)×mte×cos δ1 (3,20)
dae2
= de2+2(1+x2)×mte×cos δ2, (3,21)
где х1
и х2 – коэффициенты радиального смещения, х1 и х2 =
0
dae1
=38,3+2·2,25×cos15,82=42,6мм
dae2
=135+2·2,25·cos74,2=136,23мм
3.3.13 Определение
усилий в зацеплении
Окружные усилия
на шестерне и колесе:
Ft1
= Ft2 = (2×T1)/de1(1-0.5kbe),
(3,22)
где Ft1,
Ft2 - окружные усилия, кН;
T1-
крутящий момент на шестерне, Н • м;
de1-
делительный диаметр шестерни, мм.
Ft1
= Ft2 = 2×14,84/38,25× (1-0,5×0,285) =0,9 кН
Осевое усилие
на шестерне:
Fa1
= Ft×tgα× sinδ1
(3,23)
Fa1
= 0,9×tg200×sin15,820 = 0,09кН
Радиальное
усилие на шестерне:
Fr1
= Fttgα cos δ1 (3,24)
Fr1
= 0,9×tg200 ×cos 15,820 = 0,32 кН
Осевое усилие
на колесе:
Fa2
= Fr1 (3,25)
Fa2=0,32
кН
Радиальное
усилие на колесе:
Fr2
= Fa1 (3,26)
Fr2=
0,09 кН
3.3.14
Проверка прочности зубьев на изгиб
Для этого
определяются эквивалентные числа зубьев шестерни и колеса:
zv1
= z1/cos δ1 (3,27)
zv2
= z2/cos δ2 (3,28)
zv1
= 17/cos15,820 = 17,67 => YF1=4,31
zv2=60/cos74,180
= 220, 09=> YF2=3,74
Находим
отношения:
[σ]F1
/ YF1 и [σ]F2/ YF2 (3,29)
323,5/4,31=75,06<323.5/3,74=86,5
Проверочный
расчёт ведём по шестерне:
σF
= 2.7×103× YF×KFβ× KFV ×T/b× de ×mte×VF ≤
[σ]F, (3,30)
где VF-
коэффициент понижения изгибной прочности конической передачи по сравнению с цилиндрической:
VF = 0,85.
Коэффициент
концентрации нагрузки при изгибе KFβ определяется в зависимости
от коэффициента концентрации нагрузки по контактным напряжениям KFβ
по формуле:
KFβ
= 1+ (KHβ-1)×1.5, (3,31)
где KHβ=1,2
KFβ
= 1+(1,2-1)×1,5 = 1,3
При
определения коэффициента динамичности нагрузки КFV предварительно
необходимо определить окружную скорость колеса V, м/с:
V = π× de2(1-0.5× kbe) ×n2/6×104 (3.32)
где n2
частота вращения колеса, мин-1.
V =3.14·135·(1-0.5·0.285)·195,77/6·104
= 1,19 м/с
По скорости
назначаем степень точности: 8. По степени точности назначаем коэффициенты: KFV
= 1,04 и КHV = 1,03
σF
= 2,7·103·4,31·1,3·1,04·14,84/20·38,25·2,25·0,85=177,32МПа
σF
= 177,32<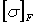 =323,5
МПа =323,5
МПа
Прочность
зубьев на изгиб обеспечена.
3.3.15
Проверка зубьев колёс на контактную прочность
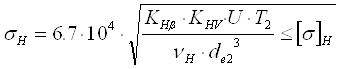 (3,33) (3,33)
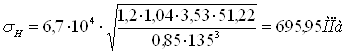
σH
= 695,95 < [σ]H = 775 МПа
Контактная
прочность зубьев обеспечена.
3.3.16
Проверка условия компоновки редуктора
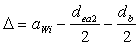 (3,34) (3,34)
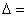 100-136,23/2-50/2=6,9
мм - условие компоновки редуктора выполняется. 100-136,23/2-50/2=6,9
мм - условие компоновки редуктора выполняется.
4. Расчёт
валов
4.1 Расчёт
входного вала
4.1.1
Проверочный расчёт вала
Составляем
расчётную схему, т.е. вал заменяем балкой на двух опорах.
К балке
прикладываем все внешние силы, нагружающие вал, приводя плоскость их действия к
двум взаимно перпендикулярным плоскостям (горизонтальной и вертикальной).
Ft1 =
0,9 кН; Fr1 = 0,32кН;
Fa1
= 0,09кН.
ΣМВ=0; Fr1·48- Fa1·d/2-RAY·26=0
RAY=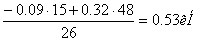
ΣМA=0; Fr1·22- Fa1·d/2+RBY·26=0
RBY=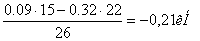
ΣF=0; RBY+
RAY -Fr1=0
0,53-0,21+0,32=0
I-I 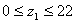
M1=Fa1·d1/2-Fr1·z1
M1=0,09×15=1,35Н·м
M1=-0,32×22+0,09×15=-5,69Н·м
II-II 
M2=-Fp·z2+
Fa1×25+ RAY×(z2-22)
M2==-0,32×22+0,09×15=-5,69 кН;
M2=-0,32·48+0,09×15+0,53×26=0
ΣМА=0; RBX·26+Ft1·22=0
RBX=-Ft1·22/26=-0,9·22/26=-0,76 кН
ΣМВ=0; -RAX·26+Ft1·48=0
RAX=Ft1·48/26=0,9×48/26=1,66 кН
ΣF=0; Ra+Rb-Ft=1,66-0,76-0,9=0
I-I 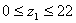
М1=-Ft1·z1
M1=0;
M1=-0,9·22=-19,8 Н·м
Выделяем
опасные сечения.
1.
Опора
А
4.1.2
Упрощённый расчёт вала
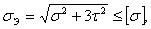 (5.4) (5.4)
где σЭ
эквивалентное нагружение, МПа;
σ
номинальные напряжения изгиба, МПа;
τ
напряжения изгиба, МПа.
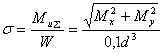 (5.5) (5.5)
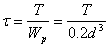
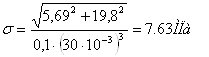
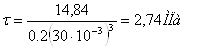
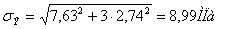
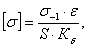 (5.6) (5.6)
где σ-1
предел выносливости материала при изгибе, МПа;
σ-1=0,43σв (5.7)
σ-1=0,43·600=258МПа
ε
коэффициент влияния абсолютных размеров поперечного сечения, ε=0,88;
S
коэффициент запаса сопротивления усталости, S=2;
Кδ
эффективный коэффициент концентрации нормальных напряжений,
Кδ
= 1,65 – переход с галтелью.
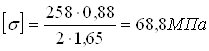
σЭ
= 8,99 < 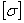 =68,8МПа =68,8МПа
Прочность в
сечении обеспечена.
4.2 Расчёт
промежуточного вала
4.2.1
Материал и термообработка вала
Так как вал
изготовляется заодно с шестерней, то материалом вала будет материал шестерни:
Сталь 40Х
σв=600МПа
σТ=350МПа
4.2.2
Проектный расчёт вала
dк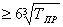 (5.11) (5.11)
dБК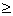 dК+3f
(5.12) dК+3f
(5.12)
dБn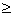 dn+3γ,
(5.13) dn+3γ,
(5.13)
dn=dK-3γ (5.14)
dк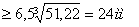
Назначаем dк=24мм,
f=1мм
dБК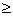 24+3·1=27мм 24+3·1=27мм
Назначаем dБК=27мм,
r=1,6мм
dn=24-3·1,6=19мм
Назначаем dn=20мм.
4.2.3
Проверочный расчёт вала
Ft1
= 0,9кН; Ft2 = 2,56кН;
Fr1
= 0,09кН; Fr2 = 0,93кН.
Fa1=0,32кН;
Т2=51,22Н·м.
ΣМA=0; RBY·129-Fr1·97-Fr2·32 +Fa1·d/2=0
RBY=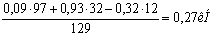
ΣМВ=0; -RAY·129+Fr1·32+Fr2·97+ Fa1·12·=0
RAY=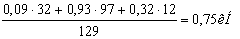
ΣF=0; Ra+
Rb-Fr1-Fr2=0
0,27+0,75-0,09-0,93=0
I-I 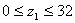
M1=Ra·z1
M1=0;
M1=0,27×32=8,64Н·м
II-II 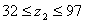
M2=Ra·z2-Fr2·(z2-32)
M2=0,27×32=8,64 Н·м
M2=0,27·97-0,93·65=-34,26
Н·м
III-III 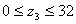
М3=Rb·z3
М3=0;
М3=0,75·32=24 Н·м
ΣМА=0; RBX·129-Ft1·97-Ft2·32=0
RBX=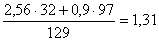 кН кН
ΣМВ=0; -RAX·129+Ft1·32+Ft2·97=0
RAX=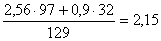 кН кН
ΣF=0; Rax+Rbx-Ft1-Ft2=0
1,31+2,15-2,56-0,9=0
I-I 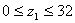
М1=Rax·z1
M1=0;
M1=2,15·32=68,8 Н·м
II-II 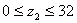
М2=Rbx·z2
M2=0;
M2=1,31·32=41,92 Н·м
Выделяем
опасные сечения.
1.
Место
посадки конического колеса на вал.
2.
Шестерня.
4.2.4
Упрощённый расчёт вала
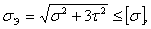 (5.15) (5.15)
где σЭ
эквивалентное нагружение, МПа;
σ
номинальные напряжения изгиба, МПа;
τ
напряжения изгиба, МПа.
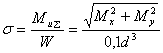 (5.16) (5.16)

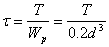 (5.17) (5.17)

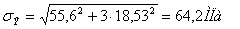
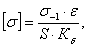 (5.18) (5.18)
где σ-1
предел выносливости материала при изгибе, МПа;
σ-1=258МПа
ε
коэффициент влияния абсолютных размеров поперечного сечения, ε=0,88;
S
коэффициент запаса сопротивления усталости, S=2;
Кδ
эффективный коэффициент концентрации нормальных напряжений,
Кδ
= 1,75 – шпоночный паз.
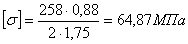
σЭ
= 64,2 <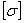 =64,87МПа =64,87МПа
Прочность в
сечении обеспечена.
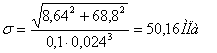
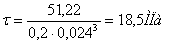
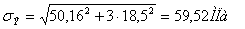
σ-1=258МПа;
ε=0,86; S=2; Кδ = 1,6 – переход с галтелью.
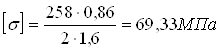
σЭ
= 59,52 <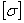 =69,33МПа =69,33МПа
Прочность в
сечении обеспечена.
4.3 Расчёт
тихоходного вала
4.3.1
Материал и термообработка вала
Сталь 45
горячекатанная.
σв=580МПа
σТ=320МПа
4.3.2
Проектный расчёт вала
d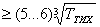 (5.19) (5.19)
dn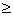 d+2t (5.20) d+2t (5.20)
dБn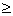 dn+3γ (5.21) dn+3γ (5.21)
dк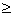 dБn dБn
d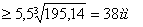
Назначаем
d=40 мм, t=2,5
dn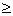 40+2·2,5=45мм 40+2·2,5=45мм
Назначаем dn=45мм;
r=3
dБn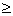 40+3·3=49мм 40+3·3=49мм
Назначаем dБn=52мм;
dк=48мм.
4.3.3
Проверочный расчёт вала
Ft2 =
2,56кН; Fr2 = 0,93кН.
ΣМA=0; RBY·129 -Fr2·93=0
RBY=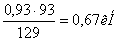
ΣМВ=0; -RAY·129+Fr2·93·=0
RAY=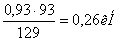
ΣF=0; Ra+
Rb-Fr2=0
0,67+0,26-0,93=0
I-I 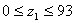
M1=Ray·z1
M1=0;
M1=0,26·93=24,18Н·м
II-II 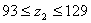
M2=
Ray·z2-
Fr2·(z2-93)
M2=33,54-92,16=-58,62
Н·м
ΣМА=0;
-Ft2·93+Rbx·129=0
RBX=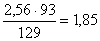 кН кН
ΣМВ=0;
-RAX·129+Ft2·36=0
RAX=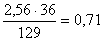 кН кН
ΣF=0; Rax+Rbx-Ft2=0
1,85+0,71-2,56=0
M=Rbx·36=1,85×36=66,6Н·м
Выделяем
опасные сечения
1.Место
посадки колеса на вал.
4.3.4
Упрощённый расчёт вала
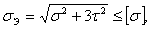 (5.23) (5.23)
где σЭ
эквивалентное нагружение, МПа;
σ
номинальные напряжения изгиба, МПа;
τ
напряжения изгиба, МПа.
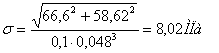
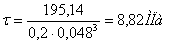
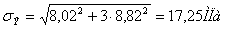
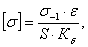 (5.24) (5.24)
σ-1=250МПа;
ε=0,81; S=2; Кδ = 1,75 – шпоночный паз.
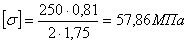
σ =
17,25<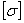 =57,86МПа =57,86МПа
Прочность в
сечении обеспечена.
5. Выбор и
расчёт подшипников качения
5.1 Расчёт
подшипников быстроходного вала
5.1.1
Выбор типа подшипников
Роликовый
конический однорядный 7206.
Сr=29,8;
Сor=22,3; e=0,36.
5.1.2
Расчёт подшипников качения
Расчёт
подшипников качения на долговечность производится по формуле:
Lh=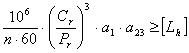 , (6.1) , (6.1)
где Lh-
расчетная долговечность подшипника, ч;
n- частота
вращения вала, об/мин;
Cr-
динамическая грузоподъёмность подшипника (берётся из справочных данных по
подшипникам), кН;
Pr-
эквивалентная нагрузка, кН;
Р- показатель
степени, равный в соответствии с результатами экспериментов для
роликоподшипников p=3,33;
а1-
коэффициент, учитывающий надежность работы подшипника, а1=1;
а23-
коэффициент, учитывающий качество металла подшипника и условия эксплуатации, а23=0,9;
[Lh]-
требуемая долговечность подшипника (для редуктора она равна сроку службы
передач tΣ=10161ч.).
Эквивалентную
нагрузку определяют по формуле:
Pr
= (X ּV ּ Fr
+Y ּ Fa) ּ Кδ ּ Кt, (6.2)
где Fr
радиальная нагрузка,кН;
Fa
осевая нагрузка, кН;
X, Y
коэффициенты радиальной и осевой нагрузок;
V
коэффициент вращения, равный 1 при вращении внутреннего кольца относительно направления
нагрузки;
Кδ
коэффициент безопасности, для редукторов Кδ = 1,3;
Кt
температурный коэффициент, вводимый при t >100º С, Кt =1.
При установке
вала на радиально-упорных подшипниках осевые силы Fa, нагружающие
подшипники, находят с учётом осевых составляющих S от действия сил Fr.
Для
конических роликоподшипников
S=0,83·e·Fr.
Rax=1,66кН, Ray=0,53кН => Ra=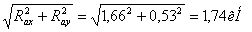
Rbx=-0,76кН, Rby=-0,21кН => Rb=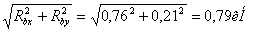
FrA=Ra=1,74кН
FrB=Rb=0,79кН
SA=0,83·0,37·1,74=0,53кН
SB=0,83·0,37·0,76=0,23кН
SA>SB;
FA≥SB-SA=>Fa1=SА; Fa2=Fa1+Fa
Fa1=0,53кН;
Fa2=0,53+0,33=0,88кН
Опора А:
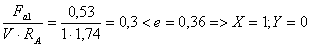
Опора В:
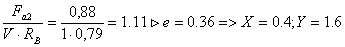
Prа = (1 · 1 ·1,74 +0) ּ 1,3 ּ
1 = 2,3 кН.
Prв = (0,4 · 1· 0,79+ 1,6 ·1) ּ 1,3 ּ
1 = 2,49 кН.
Больше перегружена
опора В.
Lh=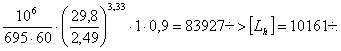
Долговечность
подшипника обеспечена.
5.2 Расчёт
подшипников промежуточного вала
5.2.1
Выбор типа подшипников
Роликовый
конический однорядный 7204.
Сr=29,2кН;
Сor=21кН; e=0,37, Y=1,6.
5.2.2
Расчёт подшипников качения
Rax=2,15кН;
Ray=0,75кН => Ra=2,28кН
Rbx=1,31кН;
Rby=0,27кН => Rb = 1,34кН.
Fra=Ra=2,28кН;
Frb=Rb=1,34кН.
SA=0,83·0,37·2,28=0,7кН
SB=0,83·0,37·1,34=0,41кН
SA<
SB; FA< SВ- SА =>Fa2=SВ; Fa1=Fa2-Fa
Fa2=0,41кН;
Fa1=0,41+0,26=0,67кН
Опора А:
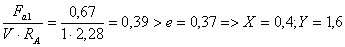
Опора В:
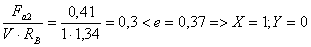
Prа = (0,4 · 1 ·2,28 +1,6·1) ּ 1,3 ּ
1 = 3,3 кН.
Prв = (1 · 1· 1,34 + 0) ּ 1,3 ּ
1 = 1,74 кН.
Больше
перегружена опора А.
Lh=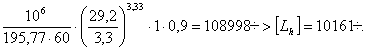
Долговечность
подшипника обеспечена.
5.3 Расчёт
подшипников тихоходного вала
5.3.1
Выбор типа подшипников
Шариковый
радиальный однорядный 209.
Сr=33,2кН;
Сor=18,6кН.
5.3.2
Расчёт подшипников качения
Rax=0,71кН;
Ray=0,26кН => Ra=0,76кН
Rbx=1,85кН;
Rby=0,67кН => Rb = 1,97кН.
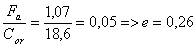
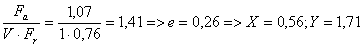
Рр=(0,56·1·0,76+1,71·1,07)·1,3·1=2,93кН.
Lh=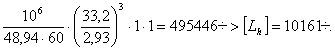
Долговечность
подшипников обеспечена.
6. Расчёт
шпоночных соединений
6.1 Расчёт
шпонки, установленной на быстроходном валу
Шпонка 8х7х60
ГОСТ 23360-78
Расчёт шпонки
на смятие
σСМ
=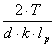 ≤
[σсм], (7.1) ≤
[σсм], (7.1)
где σСМ
напряжение смятия, МПа;
Т – вращающий
момент, Н ּм;
d – диаметр
вала, м;
lp
рабочая длина шпонки, м;
k – глубина
врезания шпонки в ступицу, м;
[ σСМ
] – допускаемое напряжение на смятие, [ σСМ ] =60 МПа.
Т=14,84Н·м;
d=20мм; lp = 50мм; к=2,8мм.
σСМ
=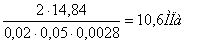 <
[σсм]=60МПа, <
[σсм]=60МПа,
6.2 Расчёт
шпонки, установленной на тихоходном валу
Т=195,14Н·м;
d=38мм; lp = 50мм; к=3,3мм.
σСМ
=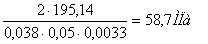 <
[σсм]=60МПа, <
[σсм]=60МПа,
Прочность
обеспечена.
7. Подбор
муфты
В
практических расчетах дополнительное нагружение упругих элементов, вызванное
радиальным смещением валов, удобнее учитывать при определении расчетного
вращательного момента:
Т=Кр·Тк,
где Кр=1,1…1,3
для муфт с пружинами сжатия и муфт со стальными стержнями.
Т=1,2·13,18=15,81кН·м
Выбираем
муфту упругау втулочно-пальцевую МУВП 16-20-I.1-I.1 УЗ ГОСТ 21423-93
Она
применяется для соединения соосных валов при передаче вращающего момента от 6,3
до 1600 Н·м и уменьшения динамических нагрузок.
Материал
полумуфт – чугун СЧ-20, сталь 35 или 35П.
Материал
пальцев – сталь 45.
Муфта
допускает значительный осевой разбег до Δ=15мм, но относительно небольшое
радиальное смещение e=0,3…0,5мм; угол перекоса валов α<1˚.
8. Выбор
смазки передач и подшипников
Для
смазывания передач и подшипников применяем картерную систему. Так как
максимальная окружная скорость колёс не превышает 2,5 м/с, а максимальные
контактные напряжения 850 МПа, следовательно по рекомендуемой кинематической
вязкости (50 мм2/с) подбираем масло И-Г-С-46 ГОСТ 17479.4-87. В
корпус редуктора заливают масло так, чтобы коническое колесо было погружено в
масло на всю ширину венца. При таком способе колёса при вращении увлекают
масло, разбрызгивая его внутри корпуса. Масло попадает на внутренние стенки
корпуса, откуда стекает в нижнюю его часть. Внутри корпуса образуется взвесь
частиц масла в воздухе, которая покрывает поверхность расположенных внутри корпуса
деталей.
Литература
1. Дунаев Л.Ф., Леликов
О.П. Конструирование узлов и деталей машин.- 4 -е изд., перераб. и доп.-М.:
Высшая школа, 1985.- 416 с.
2. Иванов М.Н. Детали.
5-е изд., перераб. –М.: Высшая школа, 1991. -383с.: илл.
3. Дунаев П.Ф. Конструирование
узлов и деталей машин: Учеб. пособие для вузов. -3-е изд., перераб. и доп.
М.: Высшая школа, 1978. – 352с., ил.
4. Черемисинов В.И.
Курсовое проектирование деталей машин: Учеб. пособие. – Киров: ВГСХА, 1998.-
163с.
|


