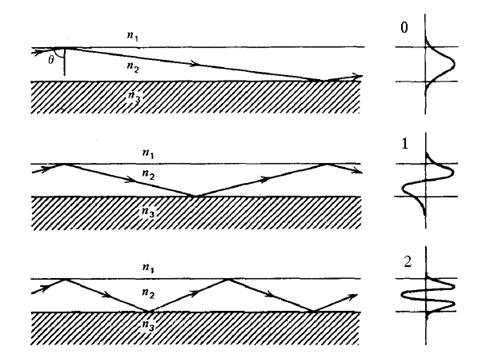
 |
|
 |
Главная
> Информатика программирование >
Курсовая работа: Разработка програмного обеспечения для расчёта дисперсионной характеристики планарного волновода
1. Введение В этой работе перед нами ставится цель научиться применять некоторые численные методы при решении метематических задач при помощи ПК. Математическое моделирование процессов и явлений в различных областях науки и техники является одним из основных способов получения новых знаний и технологических решений. Для решения поставленной в этом курсовом проекте задачи необходи иметь основные навыки программирования на языке «Pascal» и в объектно-ориентированной среде «Delphi». Эти знания могут пригодиться и в будущем, при написании каких-либо программ вычислительного характера. В данной работе необходимо написать программу, которая бы рассчитала дисперсионную характеристику планарного волновода и построила профили направляемых в нём ТЕ-мод. Для нахождения направляющих углов был использован метод дихотомии (половинного деления). Он наиболее прост в реализации, имеет относительно быструю сходимость и позволяет легко контролировать погрешность вычислений. 2. Математическое описание использованного для решения задачи МЕТОДА. Нажождение корня уравнения методом дихотомии. Считаем, что на отрезке [а, b] расположен один корень, который необходимо уточнить с погрешностью e. Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b] Х= (а + b)/2 и вычисляем функцию f(Х). Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки.Это будет отрезок [а, Х], т.е. для очередного шага уточнения точку b перемещаем в середину отрезка Х и продолжаем процесс деления как с первоначальным отрезком [а,b]. Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а,b] не станет меньше заданной погрешности e. Следует учитывать, что функция f(x) вычисляется с некоторой абсолютной погрешностью e1. Вблизи корня значения функции f(x) малы по абсолютной величине и могут оказаться сравнимыми с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в полосу шумов 2e1 и дальнейшее уточнение корня окажется невозможным. Поэтому надо задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее. Также необходимо иметь в виду, что при уменьшении интервала [а,b] увеличивается погрешность вычисления его длины (b – а) за счет вычитания близких чисел. Метод дихотомии позволяет значительно уменьшить объем вычислений по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций интервал будет равен (b - а)/2n. За 10 итераций интервал уменьшится в 2 10 =1024 раз, за 20 итераций - в 220=1048576 раз. 3. Описание алгоритма решения задачи и схема алгоритма.Основная задача, которая
решается в этой программе, это решение приведённого далее уравнения
относительно
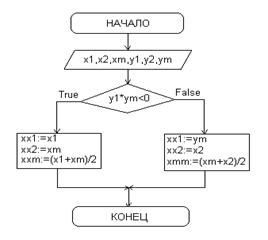
В программе решение данного уравнения реализавано методом дихотомии, схема которого приведена ниже.
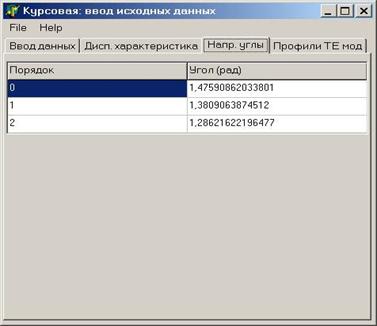
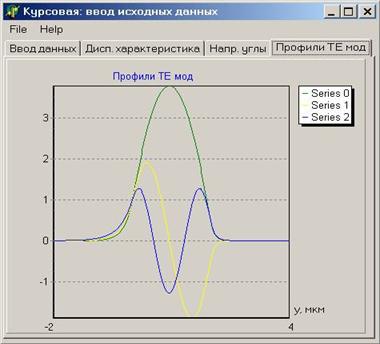
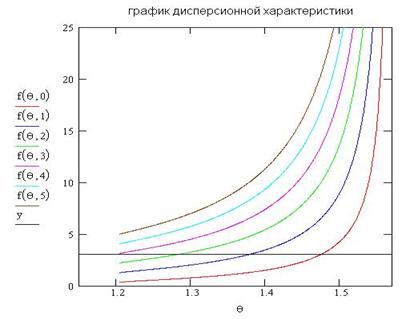
Далее, используя полученные значения направляющих углов, строится график, отображающий профили ТЕ-мод. График, отображающий правую часть уравнения (3.1), практической ценности для решения задачи не имеет и носит чисто иллюстративный характер. 4. ОПИСАНИЕ ПРОГРАММЫ.Вид программы представлен на рисунке 4.1. По своей внешней форме она представляет собой 4 закладки, расположенные на 1 форме. На первой закладке осуществляется ввод исходных данных, на второй строится график дисперсионной характеристики волновода, на третьей выводятся значения направляющих углов, а на чётвертой строятся профили ТЕ-мод.
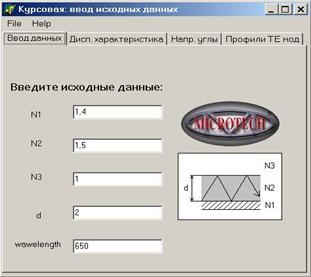
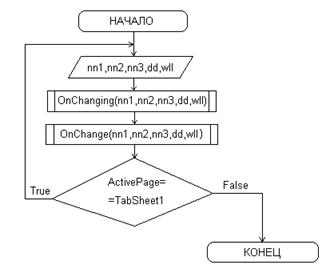
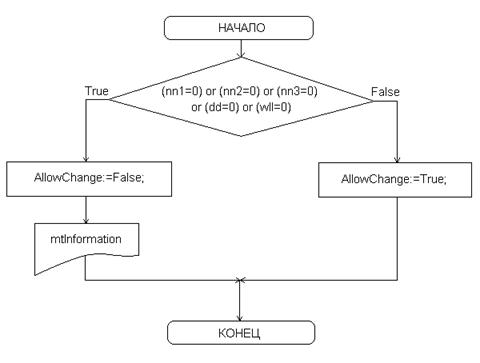
Все вычисления и построения графиков производятся при смене закладки с первой на любую другую (событие объекта TPageControl «OnChange»). Перед сменой (событие «OnChanging») осуществляется проверка на полноту исходных данных: если хоть в одном из окон осталось стоящее по умолчанию число «0», то смены закладки не произойдёт, зато возникнет информационное окно, которое укажет пользователю на его ошибку. При повторном переходе с первой закладки на другую будет произведён перерасчёт. Вычисление направляющих углов осуществляется с указанной в задании точностью – 0,001. Полная схема и листинг программы находятся в приложении А и В соответственно. 5. Результаты решения, их интерпретация и выводы по проделанной работе. 5.1. результаты работы программы. Расчёты проводились при следующих исходных данных:
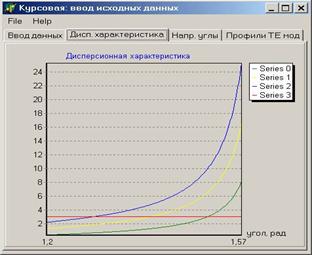
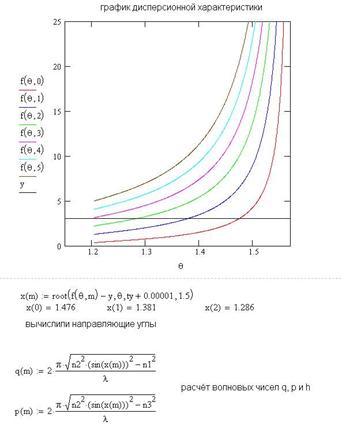
При таких введённых параметрах программа рассчитала следующую дисперсионную характеристику:
Подсчитанные направляющие углы составили:
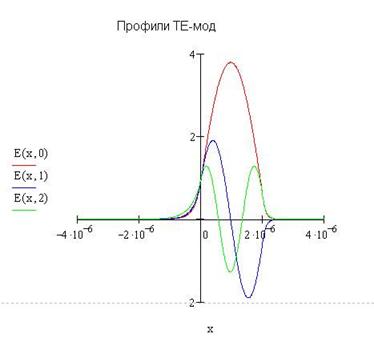
И при этих углах программа построила вот такие профили ТЕ-мод:
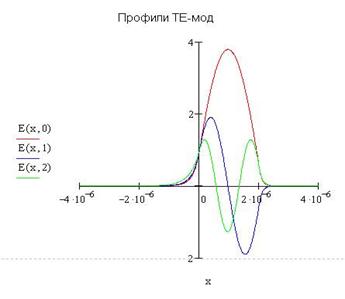
5.2. Результаты проверки в пакете «MathCAD». При аналогичных исходных данных «MathCAD» выдал следующие результаты:
Полный листинг решения поставленной задачи в пакете «MathCAD» приведён в приложении С. 5.3. Интерпретация результатов и выводы по проделанной работе. Проведя сравнительный анализ результатов, полученных при помощи написанной в «Delphi» программы и пакета «MathCAD», мы видим их полное совпадение в пределах заданной погрешности. Кроме того, конечные результаты, а именно профили ТЕ-мод, совпадают со справочными:
Из этого можно сделать вывод, что поставленная задача была решена мною верно и в полном объёме. Я не только создал конечный програмный продукт, ограниченно пригодный для практического использования, но и получил практические навыки программирования в объектно ориентированной среде «Delphi». 6. Список используемой литературы: 1. «Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль». А.Е.Мудров – МП «Раско», Томск, 1992г, 270с. 2. «Оптические волны в кристаллах». А. Ярив, П. Юх – издательство «Мир», Москва, 1987г, 616с. Приложение А. Блок-схема тела основной программы.
nn1,nn2,nn3 – показатели преломления, исходные данные, вводимые пользователем; dd – толщина волновода, вводится пользователем; wll – длина волны используемого света, вводится пользователем. Блок-схема Процедуры «OnChanging».
AllowChange – свойство объекта TPageControl, отвечающее за разрешение/неразрешение смены закладки; mtInformation – информационное окно, уведомляющее пользователя о том, что он ввёл не все исходные данные. Блок-схема Процедуры «OnChange».
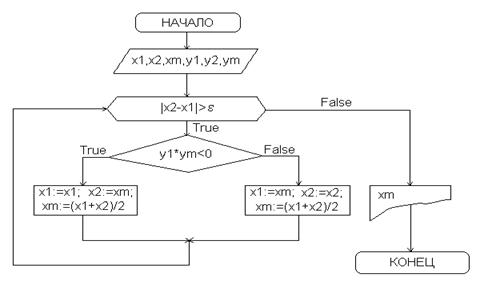
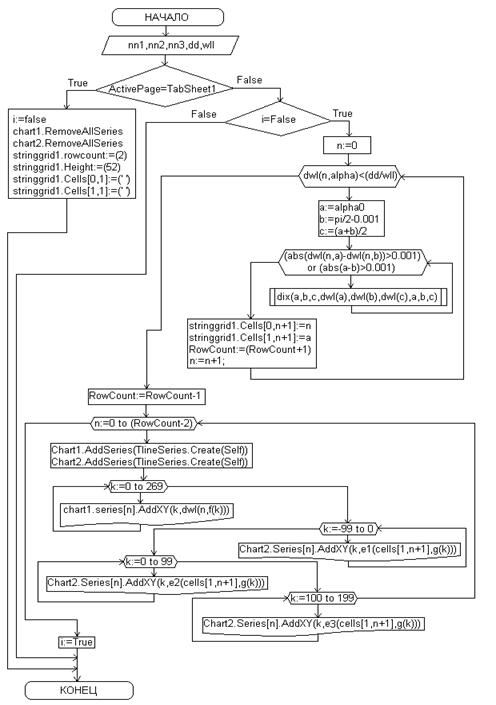
i – переменная типа boolean, которая отвечает за то, будет ли при смене закладки осуществлён пересчёт; chart1 – график, отображающий дисперсионную характеристику волновода; chart2 – график, отображающий профили ТЕ-мод; stringgrid1 – таблица, которая по ходу выполнения программы заполняется значениями направляющих углов; n – переменная типа byte, соответствующая порядку моды; a, b – переменные, задающие диапазон, на котором производится уточнение направляющих углов; dwl – функция, задающая дисперсионную характеристику волновода (численно равна правой части уравнения (3.1)); dix – процедура, осуществляющая одну итерацию метода дихотомии; k – вспомогательная переменнная типа integer, используемая для построения графика; f(k), g(k) – функции от k, выступающие в роли аргумента для других функций; e1, e2, e3 – функции, определяющие профиль моды в различных средах. Блок-схема процедуры «dix».
х1, х2, хm крайние и среднее значения интервала, на котором производится уточнение корня; y1, y2 ym значения уточняемой функции от x1, x2 и xm соответственно; xx1, xx2 , xxm новые крайние и среднее значения интервала, полученные после его уменьшения вдвое. Приложение В. Модуль формы Form1. unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, jpeg, ComCtrls, TeEngine, Series, TeeProcs, Chart,math, Grids, Menus; type TForm1 = class(TForm) PageControl1: TPageControl; TabSheet1: TTabSheet; TabSheet2: TTabSheet; Label1: TLabel; Label2: TLabel; Label3: TLabel; Label4: TLabel; Label5: TLabel; Label6: TLabel; Image1: TImage; Image2: TImage; Edit1: TEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; TabSheet3: TTabSheet; Chart1: TChart; TabSheet4: TTabSheet; Chart2: TChart; StringGrid1: TStringGrid; MainMenu1: TMainMenu; File1: TMenuItem; Exit1: TMenuItem; Help1: TMenuItem; About1: TMenuItem; Label7: TLabel; Label8: TLabel; Label9: TLabel; Label10: TLabel; Label11: TLabel; Label12: TLabel; procedure Edit1KeyPress(Sender: TObject; var Key: Char); procedure Edit2KeyPress(Sender: TObject; var Key: Char); procedure Edit3KeyPress(Sender: TObject; var Key: Char); procedure Edit4KeyPress(Sender: TObject; var Key: Char); procedure Edit5KeyPress(Sender: TObject; var Key: Char); procedure PageControl1Changing(Sender: TObject; var AllowChange: Boolean); procedure PageControl1Change(Sender: TObject); procedure FormActivate(Sender: TObject); procedure Exit1Click(Sender: TObject); procedure About1Click(Sender: TObject);
private { Private declarations } public i:boolean; nn1,nn2,nn3,dd,wll:real; { Public declarations } end; var Form1: TForm1; implementation uses Unit4; {$R *.dfm} procedure TForm1.Edit1KeyPress(Sender: TObject; var Key: Char); begin case key of '0'..'9', chr(8): ; '-': if length(edit1.text)<>0 then key:=chr(0) else key:=chr(45); '.': if pos(',',edit1.text)<>0 then key:=chr(0) else key:=chr(44); ',': if pos(',',edit1.text)<>0 then key:=chr(0) else key:=chr(44); else key:=chr(0); end; end; procedure TForm1.Edit2KeyPress(Sender: TObject; var Key: Char); begin case key of '0'..'9', chr(8): ; '-': if length(edit2.text)<>0 then key:=chr(0) else key:=chr(45); '.': if pos(',',edit2.text)<>0 then key:=chr(0) else key:=chr(44); ',': if pos(',',edit2.text)<>0 then key:=chr(0) else key:=chr(44); else key:=chr(0); end; end; procedure TForm1.Edit3KeyPress(Sender: TObject; var Key: Char); begin case key of '0'..'9', chr(8): ; '-': if length(edit3.text)<>0 then key:=chr(0) else key:=chr(45); '.': if pos(',',edit3.text)<>0 then key:=chr(0) else key:=chr(44); ',': if pos(',',edit3.text)<>0 then key:=chr(0) else key:=chr(44); else key:=chr(0); end; end; procedure TForm1.Edit4KeyPress(Sender: TObject; var Key: Char); begin case key of '0'..'9', chr(8): ; '-': if length(edit4.text)<>0 then key:=chr(0) else key:=chr(45); '.': if pos(',',edit4.text)<>0 then key:=chr(0) else key:=chr(44); ',': if pos(',',edit4.text)<>0 then key:=chr(0) else key:=chr(44); else key:=chr(0); end; end; procedure TForm1.Edit5KeyPress(Sender: TObject; var Key: Char); begin case key of '0'..'9', chr(8): ; '-': if length(edit5.text)<>0 then key:=chr(0) else key:=chr(45); '.': if pos(',',edit5.text)<>0 then key:=chr(0) else key:=chr(44); ',': if pos(',',edit5.text)<>0 then key:=chr(0) else key:=chr(44); else key:=chr(0); end; end; procedure TForm1.PageControl1Changing(Sender: TObject; var AllowChange: Boolean); begin allowchange:= tschng(strtofloat(edit1.text),strtofloat(edit2.text),strtofloat(edit3.text),strtofloat(edit4.text),strtofloat(edit5.text)); end; procedure TForm1.PageControl1Change(Sender: TObject); //основная процедура программы, привязанная к смене закладки //по её ходу и осуществляются все вычисления и построение графиков var n:byte; k:integer; a,b,c,f:real; begin nn1:=strtofloat(edit1.text); nn2:=strtofloat(edit2.text); nn3:=strtofloat(edit3.text); dd:=strtofloat(edit4.text)/1000000; wll:=strtofloat(edit5.text)/1000000000; if pagecontrol1.activepage=(tabsheet1) then begin i:=false; chart1.RemoveAllSeries; chart2.RemoveAllSeries; stringgrid1.rowcount:=(2); stringgrid1.Height:=(52); stringgrid1.Cells[0,1]:=(' '); stringgrid1.Cells[1,1]:=(' '); end else begin if i=false then begin n:=0; while dwl(n,(arcsin(nn1/nn2)+0.00005),nn1,nn2,nn3)<(dd/wll) do begin a:=(arcsin(nn1/nn2)+0.001); b:=(pi/2-0.001); c:=(a+b)/2; while (abs(dwl(n,a,nn1,nn2,nn3)-dwl(n,b,nn1,nn2,nn3))>0.001) or (abs(a-b)>0.001) do begin dix(a,b,c,(dwl(n,a,nn1,nn2,nn3)-(dd/wll)),(dwl(n,b,nn1,nn2,nn3)-(dd/wll)),(dwl(n,c,nn1,nn2,nn3)-(dd/wll)),a,b,c); end; stringgrid1.Cells[0,n+1]:=floattostr(n); stringgrid1.Cells[1,n+1]:=floattostr(a); stringgrid1.RowCount:=(stringgrid1.RowCount+1); if n<14 then stringgrid1.Height:=(stringgrid1.Height+26); n:=n+1; end; stringgrid1.RowCount:=(stringgrid1.RowCount-1); stringgrid1.Height:=(stringgrid1.Height-26); for n:=0 to (stringgrid1.RowCount-2) do begin Chart1.AddSeries( TlineSeries.Create( Self ) ); chart1.Serieslist[n].SeriesColor:=chart1.getfreeseriescolor(false); for k:=0 to 269 do begin f:=(arcsin(nn1/nn2)+k*(((pi/2)-0.001-arcsin(nn1/nn2))/300)); chart1.Series[n].AddXY(k,dwl(n,f,nn1,nn2,nn3),'',clteecolor); end; end; Chart1.AddSeries( TlineSeries.Create( Self ) ); for k:=1 to 269 do begin chart1.Series[chart1.SeriesCount-1].AddXY(k,(dd/wll),'',clteecolor); end; for n:=0 to (stringgrid1.RowCount-2) do begin Chart2.AddSeries( TlineSeries.Create( Self ) ); chart2.Serieslist[n].SeriesColor:=chart2.getfreeseriescolor(false); for k:=(-99) to 0 do begin chart2.Series[n].AddXY(k,e1(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.Cells[1,n+1]),(k*dd/100)),'',clteecolor); end; for k:=0 to 99 do begin chart2.Series[n].AddXY(k,e2(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.cells[1,n+1]),(k*dd/100)),'',clteecolor); end; for k:=100 to 199 do begin chart2.Series[n].AddXY(k,e3(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.Cells[1,n+1]),(k*dd/100)),'',clteecolor); end; end; label7.Caption:=floattostrf(arcsin(nn1/nn2),ffgeneral,3,3); label8.caption:=floattostrf((pi/2-0.001-(pi/2-arcsin(nn1/nn2))/300),ffgeneral,3,3); label10.Caption:=floattostr(-dd*1000000); label11.Caption:=floattostr(2*dd*1000000); i:=true; end; end; end; procedure TForm1.FormActivate(Sender: TObject); begin i:=false; stringgrid1.Cells[0,0]:=('Порядок'); stringgrid1.Cells[1,0]:=('Угол (рад)'); end; procedure TForm1.Exit1Click(Sender: TObject); begin close; end; procedure TForm1.About1Click(Sender: TObject); begin messagedlg('Курсовая работа по информатике, ТУСУР,' +#13+' 1 курс, специальность 210405.' +#13+' Выполнил студент группы 164' +#13+' Филатов Александр.', mtinformation, [mbOK],0); end; end. Вспомогательный модуль, содержащий математические процедуры и функции. unit Unit4; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ExtCtrls, jpeg, ComCtrls, TeEngine, Series, TeeProcs, Chart,math; function tschng(n1,n2,n3,d,wl:real):boolean; function dwl(m:byte; tetta,n1,n2,n3:real):real; function q(wl,tetta,n2,n1:real):real; function h(wl,tetta,n2:real):real; function p(wl,tetta,n2,n3:real):real; function e1(wl1,d1,n11,n21,n31,tetta1,x1:real):real; function e2(wl2,d2,n12,n22,n32,tetta2,x2:real):real; function e3(wl3,d3,n13,n23,n33,tetta3,x3:real):real; procedure dix(x1,x2,xm,y1,y2,ym:real; var xx1,xx2,xxm:real); implementation function tschng(n1,n2,n3,d,wl:real):boolean; //осуществляет проверку исходных данных на полноту begin if (n1=0) or (n2=0) or (n3=0) or (d=0) or (wl=0) then begin messagedlg('Вы должны ввести значения всех параметров!', mtinformation, [mbOK],0); tschng:=(False); end else tschng:=(True); end; function dwl(m:byte; tetta,n1,n2,n3:real):real; //функция дисперсионной характеристики волновода var aa,bb,cc,dd: real; begin aa:= sqrt(1-sqr(sin(tetta))); aa:= 1/(2*pi*n2*aa); bb:= sqrt(sqr(n2*sin(tetta))-sqr(n3)); cc:= sqrt(sqr(n2*sin(tetta))-sqr(n1)); dd:= n2*sqrt(1-sqr(sin(tetta))); dwl:=aa*(arctan(bb/dd)+arctan(cc/dd)+pi*m); end; function q(wl,tetta,n2,n1:real):real; //функция, вычисляющая волновое число q begin q:=(2*pi*sqrt(sqr(n2*sin(tetta))-n1*n1))/wl; end; function h(wl,tetta,n2:real):real; //функция, вычисляющая волновое число h begin h:=(2*pi*cos(tetta)*n2)/wl; end; function p(wl,tetta,n2,n3:real):real; //функция, вычисляющая волновое число p begin p:=(2*pi*sqrt(sqr(n2*sin(tetta))-n3*n3))/wl; end; function e1(wl1,d1,n11,n21,n31,tetta1,x1:real):real; //функция, задающая профиль Еу ТЕ моды при условии х<=0 begin e1:=exp(q(wl1,tetta1,n21,n11)*x1); end; function e2(wl2,d2,n12,n22,n32,tetta2,x2:real):real; //функция, задающая профиль Еу ТЕ моды при условии 0<х<d begin e2:=(q(wl2,tetta2,n22,n12)/h(wl2,tetta2,n22))*(sin(x2*h(wl2,tetta2,n22))+(h(wl2,tetta2,n22)/q(wl2,tetta2,n22,n12))*cos(h(wl2,tetta2,n22)*x2)); end; function e3(wl3,d3,n13,n23,n33,tetta3,x3:real):real; //функция, задающая профиль Еу ТЕ моды при условии х>=d begin e3:=(q(wl3,tetta3,n23,n13)/h(wl3,tetta3,n23))*(sin(d3*h(wl3,tetta3,n23))+(h(wl3,tetta3,n23)/q(wl3,tetta3,n23,n13))*cos(h(wl3,tetta3,n23)*d3))*exp(-p(wl3,tetta3,n23,n33)*(x3-d3)); end; procedure dix(x1,x2,xm,y1,y2,ym:real; var xx1,xx2,xxm:real); //процедура, осуществляющая 1 итерацию метода дихотомии begin if (y1*ym)<0 then begin xx1:=x1; xx2:=xm; xxm:=(x1+xm)/2; end; if (ym*y2)<0 then begin xx1:=xm; xx2:=x2; xxm:=(xm+x2)/2; end; end; end. Приложение c.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, x£0
,
- поперечные волновые числа
1, 2 и 3-й сред соответственно.
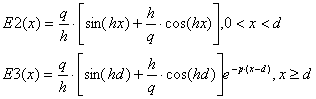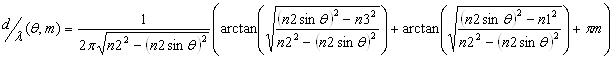где n1, n2, n3 – показатели преломления трех сред;
: 
, (3.1)
- толщина волновода;
- длина волны запускаемого пучка света;
- направляющий угол;
- порядок моды;
- показатели преломления волновода и окружающих его
веществ.
