Информатика программирование : Курсовая работа: Распределение ресурсов по трем отраслям
Курсовая работа: Распределение ресурсов по трем отраслям
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"САРОВСКИЙ ГОСУДАРСТВЕННЫЙ ФИЗИКО-ТЕХНИЧЕСКИЙ
ИНСТИТУТ"
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ
На тему:
СТУДЕНТ (группа ИС-45Д)
РУКОВОДИТЕЛЬБеляев С.П.
г. Саров 2008 г
Оглавление
ВВЕДЕНИЕ. 3
ТЕОРЕТИЧЕСКАЯ
ЧАСТЬ. 4
Исходные
параметры.. 5
Искомые
параметры.. 6
МЕТОД
РЕШЕНИЯ.. 6
ОБОСНОВАНИЕ
ВЫБОРА ПРОГРАММНЫХ СРЕДСТВ.. 9
ОПИСАНИЕ
ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛЯ.. 10
СПИСОК
ЛИТЕРАТУРЫ.. 11
ВВЕДЕНИЕ
Основная часть данной
работы направлена на практическое освоение метода динамического
программирования на примере решения хорошо изученных задач, а именно:
простейшей задачи оптимального распределения ресурсов и задачи управления запасами
продукта при случайном спросе на него.
Кроме
теоретических основ и практических рекомендаций, необходимых для численного
решения указанных задач, связанных с простым классом одномерных процессов
распределения [1], дополнительно рассматриваются задачи оптимального
распределения при наличии двух типов ресурсов и двух типов ограничений, в
рамках которых возможны не только постановка и решение большого числа
прикладных задач [1, 5], но также выявление существенных и качественных
особенностей, связанных с применением метода динамического программирования,
при переходе к задачам с многомерными процессами распределения.
Цель работы: знакомство с постановкой задачи оптимального распределения
ограниченного ресурса и методом множителей Лагранжа в задачах условной
оптимизации, изучение принципа оптимальности Беллмана и вычислительной схемы
решения задачи оптимального распределения ограниченного ресурса методом
динамического программирования, разработка программы для численного решения
задачи и проведение расчетов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Постановка
простейшей задачи оптимального распределения
ограниченного
ресурса
В
различных производственно-экономических системах значительное число решаемых
задач тесно связано с эффективным использованием и распределением ограниченных
ресурсов, необходимых для нормального функционирования таких систем. Переходя к
формулировке одной из простейшей задач такого класса, вначале опишем кратко
процессы, обусловливающие возникновение этого типа задач.
Пусть
некоторая производственно-экономическая система располагает заданным
количеством какого-либо экономического ресурса, под которым подразумеваются
материальные, трудовые, финансовые либо иные ресурсы, необходимые для
функционирования системы. В случае нескольких потребителей указанного ресурса
или далее соответствующих технологических процессов возникает следующая задача:
разделить имеющееся количество ресурса между ними так, чтобы максимизировать их
суммарную эффективность или получаемый доход от этих процессов [1].
Для
математической постановки этой задачи требуется принять следующие основные
предположения [1]:
1)
эффективности каждого из рассматриваемых технологических процессов, например в
виде соответствующих доходов, могут быть измерены общей единицей: либо в виде
валового выпуска однородного продукта, либо в стоимостной форме;
2)
эффективность каждого технологического процесса не зависит от
того,
какие количества ресурсов были выделены для других технологических процессов;
3)
общая эффективность или, что то же самое, суммарный доход от всех технологических
процессов – аддитивная величина, то есть величина, равная сумме доходов,
получаемых от каждого процесса в отдельности.
Тогда математическая постановка задачи
оптимального распределения ограниченного ресурса формулируется
следующим образом [1].
Предположим,
что имеется N
технологических
процессов, занумерованных в определенном порядке числами 1, 2, ... , N , и каждому такому процессу
поставлена в соответствие некоторая функция, оценивающая его эффективность, а
именно: величина дохода в зависимости от количества выделенного ресурса для
этого процесса. Пусть xi
количество выделенного ресурса i-му процессу (i = 1, 2, ... , N ), а величина дохода,
получаемого в этом процессе, задается функцией gi
= gi
(xi
) .
Отметим, что в качестве таких функций можно выбирать, например,
производственные функции или функции полезности неоклассического типа [2, 3].
С
учетом второго и третьего предположения – о независимости процессов и
аддитивности их общей эффективности – для суммарного дохода от распределения
ограниченного ресурса между указанными N технологическими процессами получим
следующее выражение:
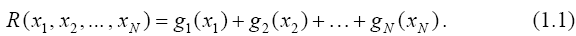
В
силу ограниченности распределяемого ресурса, располагаемое количество которого
здесь обозначим через z, для переменных задачи xi
, i = 1, 2, ... , N , имеет место следующее
ограничение:

которое
вместе с условиям неотрицательности для этих же переменных

задает
допустимую
область определения
для функции (1.1). Таким образом, задача оптимального распределения
ограниченного ресурса заключается в том, чтобы определить значения переменных xi
, i = 1, 2, ... , N , которые доставляют
максимальное значение функции R(x1, x2 , ... , xN
)
(1.1), удовлетворяя при этом ограничениям (1.2), (1.3). Задача (1.1) - (1.3)
относится к классу задач условной оптимизации. Ограничения, задающие в этих
задачах допустимые множества, обычно в математической экономике разделяют на
две группы, а именно: ограничения вида (1.2) относят к функциональным
ограничениям,
а ограничения вида (1.3) – к прямым ограничениям [2].
Значения xi
, i = 1, 2, ... , N , для которых
доставляется максимальное значение функции (1.1) с учетом (1.2), (1.3),
называют решением задачи, а соответствующие значения функции (1.1),
то есть max
R(x1, x2 , ... , xN
) , – значением
задачи.
Если ограничения задачи, заданные в виде нестрогих неравенств, для ее решения
обращаются в равенства, то такие ограничения тогда называют эффективными; иначе эти ограничения
являются неэффективными, и в связи с этим их
можно в процессе решения задачи отбрасывать.
1.
z – располагаемое количество ресурса,
2.
n – мера квантования z
3.
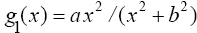
4.
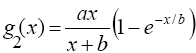
5.
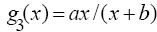
1.
fN
(z) = fN (nΔ ) - искомый максимум функции R
2.
xN
(z)
искомое оптимальное количество ресурса
МЕТОД РЕШЕНИЯ
Переходя к изложению вычислительной схемы
решения задачи с применением основного функционального уравнения (1.15), предположим
(а это существенно для дальнейшего изложения), что переменные задачи N i xi
, ...
2, 1, , = , а также количества
распределяемого ресурса 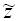 как в (1.10), так и в (1.15) могут
принимать только дискретные значения с некоторым выбранным шагом Δ >0. То есть имеет место: как в (1.10), так и в (1.15) могут
принимать только дискретные значения с некоторым выбранным шагом Δ >0. То есть имеет место:

где
nΔ = z . Соответственно,
функции (1.10) в рекуррентном соотношении (1.15) будут вычисляться только для
указанных в (1.16) значений 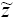 или, что то же самое,
только для таких точек: или, что то же самое,
только для таких точек:
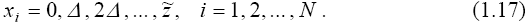
Указанный
подход позволяет избежать процедуры интерполирования при вычислении значений 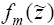 , исходя из
вычисленных значений fm−1( y) в точках y = 0, Δ , 2Δ , ... , z . Действительно, для вычисления под знаком
максимума в (1.15) значения , исходя из
вычисленных значений fm−1( y) в точках y = 0, Δ , 2Δ , ... , z . Действительно, для вычисления под знаком
максимума в (1.15) значения 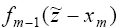 − интерполирования не требуется, так как здесь с
учетом (1.16) и (1.17) имеет место: − интерполирования не требуется, так как здесь с
учетом (1.16) и (1.17) имеет место: 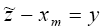 . .
Согласно
(1.15), для вычисления 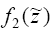 вначале следует найти значения вначале следует найти значения 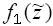 для всех
значений для всех
значений 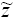 из (1.16) с помощью
соотношений (1.12) из (1.16) с помощью
соотношений (1.12)
или
(1.13), которые доставляют множество всех требуемых значений
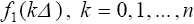 . Затем для
всех . Затем для
всех 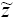 (1.16) с учетом (1.15)
вычисляются значения: (1.16) с учетом (1.15)
вычисляются значения:
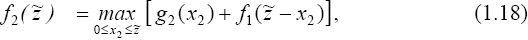
где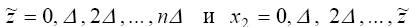 .Процедура максимизации
(1.18) заключается в том, чтобы вначале для каждого z ~ последовательно вычислить
значения: .Процедура максимизации
(1.18) заключается в том, чтобы вначале для каждого z ~ последовательно вычислить
значения: 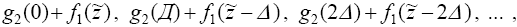 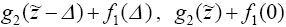 а
затем выбрать из них максимальное, то есть искомое значение а
затем выбрать из них максимальное, то есть искомое значение 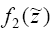 ; при этом определяется
и соответствующее ему оптимальное значение ; при этом определяется
и соответствующее ему оптимальное значение 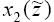 . .
Получив
множество значений 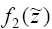 для для 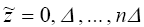 , можно приступить к вычислению
функции , можно приступить к вычислению
функции 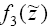 исходя
из (1.15) при m
=3: исходя
из (1.15) при m
=3:
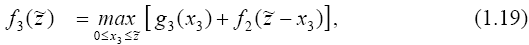
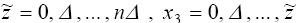 и т.д. для остальных
m = 4, 5, ... , N . и т.д. для остальных
m = 4, 5, ... , N .
Таким
образом, в процессе решения уравнения (1.15) для m = 2, 3, ... , N
последовательно
заполняется таблица, подобная табл. 1.1.
Таблица
1.1
Оптимальные
доходы в зависимости от количества процессов
и
выделенного ресурса
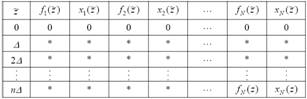
С
заполнением последних двух столбцов указанной таблицы решение
задачи
фактически получено. Действительно, поскольку функция 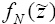 по построению монотонно
неубывающая по по построению монотонно
неубывающая по 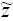 , постольку fN
(z) = fN
(nΔ ) - искомый максимум
функции R
(1.1),
а xN
(z) – искомое оптимальное
количество ресурса, выделенное для N-го процесса. Стало быть, оставшееся
количество ресурса, равное z − xN (z) , должно быть распределено
оптимальным образом между остальными процессами. Соответствующее решение, то
есть оптимальный доход (1.10) для первых N −1 процессов, находится в столбце с заголовком , постольку fN
(z) = fN
(nΔ ) - искомый максимум
функции R
(1.1),
а xN
(z) – искомое оптимальное
количество ресурса, выделенное для N-го процесса. Стало быть, оставшееся
количество ресурса, равное z − xN (z) , должно быть распределено
оптимальным образом между остальными процессами. Соответствующее решение, то
есть оптимальный доход (1.10) для первых N −1 процессов, находится в столбце с заголовком 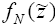 − , а именно: в строке, отвечающей
значению − , а именно: в строке, отвечающей
значению 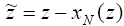 .
В этой же строке в столбце с заголовком .
В этой же строке в столбце с заголовком 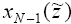 − находится величина
оптимального количества ресурса, который выделяется для (N −1)-го процесса. Таким
образом, перемещаясь по столбцам табл. 1.1 справа налево (это т.н. обратный ход
[1, 3]), можно последовательно определить все значения − находится величина
оптимального количества ресурса, который выделяется для (N −1)-го процесса. Таким
образом, перемещаясь по столбцам табл. 1.1 справа налево (это т.н. обратный ход
[1, 3]), можно последовательно определить все значения 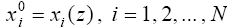 , которые доставляют
абсолютный максимум функции R(x1, x2 , ... , xN
) (1.1)
в области (1.2), (1.3) для заданного количества распределяемого ресурса – z, конечно же, с учетом
дополнительных ограничений (1.16), (1.17) , которые доставляют
абсолютный максимум функции R(x1, x2 , ... , xN
) (1.1)
в области (1.2), (1.3) для заданного количества распределяемого ресурса – z, конечно же, с учетом
дополнительных ограничений (1.16), (1.17)
ОБОСНОВАНИЕ ВЫБОРА
ПРОГРАММНЫХ СРЕДСТВ
Курсовая
работа выполнена с помощью программы Microsoft Office Excel, одной из наиболее передовых,
мощных и современных сред разработки Windows-приложений и электронных таблиц.
Встроенное средство поиска решений позволяет быстро справиться с задачей о распределения
ресурсов.
ОПИСАНИЕ ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛЯ
Для
начала работы с программой следует задать n и z и нажать
кнопку определить
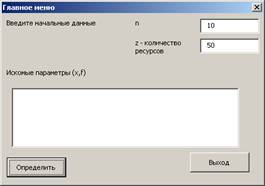
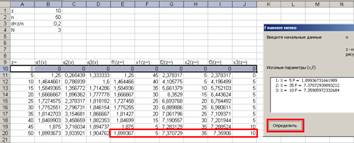
После
этого программа создаст таблицы.
СПИСОК ЛИТЕРАТУРЫ
1. Беллман, Р.
Прикладные задачи динамического программирования /Р. Беллман, С. Дрейфус. – М.:
Наука, 1965. – 460 с.
2. Ланкастер, К. Математическая экономика / К. Ланкастер.
М.: Советское радио, 1972. – 464 с.
3. Колемаев, В.А. Математическая экономика / В.А. Колемаев.
М.:
ЮНИТИ, 1998. – 240 с.
4. Беллман, Р. Процессы регулирования с адаптацией / Р.
Беллман. – М.: Наука, 1964. – 360 с.
5. Первозванский, А.А. Математические модели в управлении
производством / А.А. Первозванский. – М.: Наука, 1975. – 616 с.
6. Калихман, И.Л. Динамическое
программирование в примерах и задачах / И. Л. Калихман, М. А. Войтенко. – М.:
Высшая школа, 1979. – 125 с.
ТЕКСТ ПРОГРАММЫ
Public Function f_g1(x As Double) As Double
f_g1 = 2.5 * Sqr(x) / (Sqr(x) + 1)
End Function
Public Function f_g2(x As Double) As Double
f_g2 = 6 * x * (1 - Exp(-x / 4)) / (x + 4)
End Function
Public Function f_g3(x As Double) As Double
f_g3 = 2 * x / (x + 0.5)
End Function
Private Sub CommandButton1_Click()
Dim i As Integer
Dim n As Integer
Dim z As Double
Dim d As Double
Dim m_str As String
Range("A1").Select
n = Val(TextBox1.Text)
z = Val(TextBox2.Text)
d = z / n
ActiveCell.Cells(1, 2) = n
ActiveCell.Cells(2, 2) = z
Range("A11").Select
For i = 1 To 100
For j = 1 To 10
ActiveCell.Cells(i, j) = ""
Next
Next
For i = 1 To 10
ActiveCell.Cells(0, i) = 0
Next
For i = 1 To n
ActiveCell.Cells(i, 1) = i * d
ActiveCell.Cells(i, 2) = f_g1(i + 0#)
ActiveCell.Cells(i, 3) = f_g2(i + 0#)
ActiveCell.Cells(i, 4) = f_g3(i + 0#)
ActiveCell.Cells(i, 5) = f_g1(i + 0#)
Next
For i = 1 To n
ActiveCell.Cells(i + 0, 7) = GetF2Val(i + 0, d)
ActiveCell.Cells(i + 0, 8) = Int(GetF2Pos(i + 0, d) * d)
ActiveCell.Cells(i + 0, 9) = GetF3Val(i + 0, d)
ActiveCell.Cells(i + 0, 10) = Int(GetF3Pos(i + 0, d) * d)
ActiveCell.Cells(i + 0, 6) = Abs(z - ActiveCell.Cells(i + 0, 8)
- ActiveCell.Cells(i + 0, 10))
Next
ListBox1.Clear
For i = 1 To 3
m_str = Str(i) + ": X = " + Str(ActiveCell.Cells(n + 0,
4 + i * 2)) + " F = " + Str(ActiveCell.Cells(n + 0, 3 + i * 2))
ListBox1.AddItem (m_str)
Next
Range("A10:J10").Select
End Sub
Private Sub CommandButton2_Click()
Hide
End Sub
Public Function GetF2Val(n As Integer, d As Double) As Double
Dim maxs As Double
maxs = f_g2(0) + f_g1(n * d)
For i = 1 To n
If f_g2(i * d) + f_g1((n - i) * d) >= maxs Then
maxs = f_g2(i * d) + f_g1((n - i) * d)
End If
Next
GetF2Val = maxs
End Function
Public Function GetF2Pos(n As Integer, d As Double) As Integer
Dim maxs As Double
Dim maxp As Integer
Range("A11").Select
maxs = f_g2(0) + f_g1(n * d)
max_p = 0
For i = 1 To n
If f_g2(i * d) + f_g1((n - i) * d) >= maxs Then
maxs = f_g2(i * d) + f_g1((n - i) * d)
maxp = i
End If
Next
GetF2Pos = maxp
End Function
Public Function GetF3Val(n As Integer, d As Double) As Double
Dim maxs As Double
maxs = f_g3(0) + f_g2(n * d)
For i = 1 To n
If f_g3(i * d) + f_g2((n - i) * d) >= maxs Then
maxs = f_g3(i * d) + f_g2((n - i) * d)
End If
Next
GetF3Val = maxs
End Function
Public Function GetF3Pos(n As Integer, d As Double) As Integer
Dim maxs As Double
Dim maxp As Integer
Range("A11").Select
maxs = f_g3(0) + f_g2(n * d)
max_p = 0
For i = 1 To n
If f_g3(i * d) + f_g2((n - i) * d) >= maxs Then
maxs = f_g3(i * d) + f_g2((n - i) * d)
maxp = i
End If
Next
GetF3Pos = maxp
End
Function
|


