Информатика программирование : Курсовая работа: Прикладна теорія цифрових автоматів
Курсовая работа: Прикладна теорія цифрових автоматів
ЗМІСТ
Введення
1. Вибір варіанта завдання
1.1. Граф-схема автомата Мура
1.2. Граф-схема автомата Мілі
2. Основна частина
2.1. Структурний синтез автомата Мура
2.1.1. Кодування станів
2.1.2. Функції збудження тригерів та вихідних сигналів
2.1.3. Переведеня у базис
2.2.Структурний синтез автомата Мілі
2.1.1. Кодування станів
2.1.2. Функції збудження тригерів та вихідних сигналів
2.1.3. Переведеня у базис
Висновок
Список використаної літератури
1.ВИБІР ВАРІАНТА ЗАВДАННЯ
1.1. Граф-схема алгоритму
Граф-схема складається з чотирьох блоків E, F, G, H і вершин “BEGIN” та “END”. Кожен з блоків
має два входи (А, В) і два виходи (C, D). Я вибираю блоки E, F, G, H з п’яти блоків з номерами 0, 1, 2, 3, 4 (вони подаються в п.5 на
рис.3-7 у методичних вказівках) на підставі чисел А, В, С, А+В+С (де А – число,
В – місяць народження, С – номер студента в журналі), за такими правилами:
-
блок “Е” має схему блока за номером А(MOD 5);
-
блок “F” має схему блока за номером B(MOD 5);
-
блок “G” має схему блока за номером C(MOD 5);
-
блок “H” має схему блока за номером (А+B+C)(MOD 5).
В моєму варіанті:
А=30;
В=06;
С=22.
“Е”: А(MOD 5)=30(MOD 5)=0;
“F”: B(MOD 5)=06(MOD 5)=1;
“G”: C(MOD 5)=22(MOD 5)=2;
“H”: (А+B+C)(MOD
5)=(30+06+22)(MOD 5)=58(MOD 5)=3.
Блоки E, F, G, H з’єднуються між собою
згідно зі структурною схемою графа, яка показана на рис. 10 у методичних
вказівках.
Згідно з моїм варіантом завдання, граф-схема автомата має такий вигляд:
 
BEGIN
   
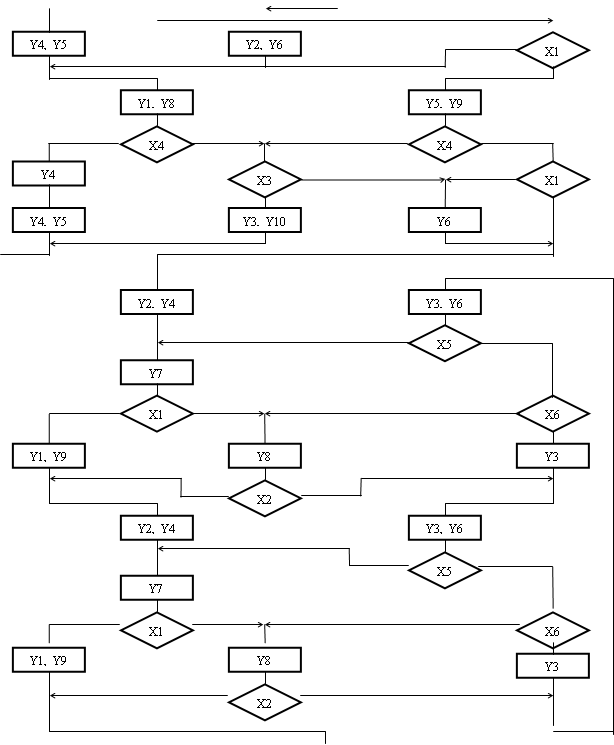

END
Рис.1.1. Граф-схема алгоритму автомата Мілі

BEGIN
 
         
   
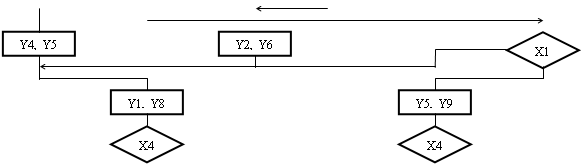
      
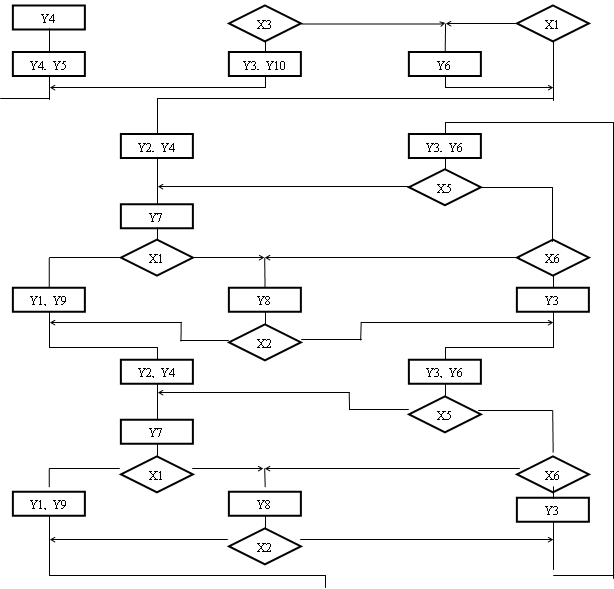

END
Рис.1.2. Граф-схема алгоритму автомата Мура
1.2. Тип тригера
Тип тригера вибирається за значенням числа A(MOD 3) на підставі табл.2 в методичних вказівках. Згідно з моїм варіантом
завдання:
A(MOD 3)=30(MOD 3) =0.
Тому, згідно таблиці 2 у методичних вказівках, тип тригера
в моєму завданні для синтезу автомата Мура – D, а для синтезу автомата Мілі – Т.
1.3. Серія інтегральних мікросхем
Серія інтегральних мікросхем для побудови принципових схем
синтезованих автоматів для мого варіанта завдання – КР1533.
2. ОСНОВНА ЧАСТИНА
2.1. Структурний синтез автомата Мілі
2.1.1. Розмітка станів ГСА
На етапі одержання відміченої ГСА входи вершин, які слідують за
операторними, відмічають символами a1, a2, ... за наступними правилами:
1) символом а1 відмічають вхід вершини, яка слідує за
початковою, а також вхід кінцевої вершини;
2) входи усіх вершин , які слідують за операторними, повинні бути
відмічені;
3) входи різних вершин, за винятком кінцевої, відмічаються різними
символами;
4) якщо вхід вершини відмічається, то тільки одним символом.
За ціми правилами в мене вийшло 22 стани (а22).
2.1.2. Таблиця переходів автомата
Для кожного стану ai визначаю по ГСА всі шляхи, які ведуть в інші стани і проходять
обов’язково тільки через одні операторну вершину. Виняток становить перехід в
кінцевий стан (вершину).
Для мікропрограмних автоматів таблиці переходів-виходів
будуються у вигляді списку, тому що велика кількість станів. Розрізняють пряму
та зворотну таблицю переходів. Зворотна таблиця переходів будується для D-тригера. Для автомата Мілі я буду будувати
пряму таблицю переходів.
|
Am
Kam
as
Kas
Xamas
Yamas
T1
T2
T3
T4
T5
|
a1
10110
a2
10010
1
Y1Y4
T3
|
a2
10010
|
a4 |
a6
00010
|
10000
X3
|
X3
Y2Y6
|
Y7
T1
|
|
T4 |
A |
B |
|
a3
00011
a4
00010
1
Y2Y6
T5
|
a4
00010
a5
00000
1
Y1Y8
T4
|
a5
00000
a8
|
a9 |
a11
01000
|
01001 |
10001
X4
|
X4X3 |
X4X3
Y4
|
Y3Y10 |
Y6 |
|
|
T1
T2
|
T2 |
|
|
T5 |
T5
C
|
D |
E |
a6
10000
a5
|
a7
00000
|
11001
X1
|
X1 Y1Y8 |
|
Y5Y9
T1
|
T2 |
T5
F
|
G |
a7
11001
a9
|
a11 |
a11 |
a12
01001
|
10001 |
10001 |
11000
X4X3
|
X4X3 |
| X4X1 |
X4X1
Y3Y10
|
Y6 |
Y6 |
Y2Y4
T1
|
|
T2 |
T2 |
|
|
T5
H
|
I |
| J |
K |
a8
01000
a9
01001
1
Y4Y5
T5
|
a9
01001
a10
00001
1
Y1Y2
T2
|
|
|
|
|
|
|
|
|
Табл.1. Таблиця переходів Т-тригера
2.1.3. Кодування
станів
Аналіз канонічного методу структурного синтезу
автомата показує, що різні варіанти кодування станів автомата приводять до
різних виражень функцій збудження пам'яті і функцій виходів, у результаті чого
складність комбінаційної схеми істотно залежить від обраного кодування.
Я буду кодувати стани автомату з допомогою
евристичного алгоритму кодування, тому що я синтезую автомат на базі Т-тригера.
Даний алгоритм мінімізує сумарне число
переключень елементів пам'яті на всіх переходах автомата і використовується для
кодування станів автомата при синтезі на базі T, RS, JK-тригерів. Для даних
типів тригерів (на відміну від D-тригерів) на кожнім переході, де тригер зміню
своє значення на протилежне, одна з функцій збудження обов'язково дорівнює 1.
Зменшення числа переключень тригерів приводить до зменшення кількості одиниць
відповідних функцій збудження, що при відсутності мінімізації однозначно
приводить до спрощення комбінаційної схеми автомата.
Будую матрицю |T|, яка
складається із всіх пар номерів (i, j), для яких P(i,
j) ¹ 0, ij. Для кожної пари вказуємо її вагу.
i j P(i, j)
1
2 1
2
4 1
2
6 1
3
4 1
4
5 1
5
8 1
5
9 1
5
10 1
5
11 1
6
5 1
6
7 1
7
9 1
7
11 2
7
12 1
8
9 1
9
10 1
10
3 1
10
7 1
10
4 1
10
5 1
T=
11 12 1
12
13 1
13
14 1
13
15 1
14
17 1
15
17 1
15
19 1
16
19 1
17
18 1
18
1 1
18
20 1
19
18 1
19
20 1
19
21 1
20
1 1
20
22 1
21
22 1
22
13 1
22
15 1
22 16 1
Далі, за допомогою програми ECODE
3, виконую кодування станів автомата на ЕОМ. При цьому вказую
глибину кодування (від 4 до 6) та вибираю те кодування, коефіцієнт якого ближче
до 1 (у мене коефіцієнт кодування 1,26). Результати кодування заношу до таблиц
1. Ось кінцеві результати кодування:
Підрахунок ефективності кодування:
Кількість переключень тригерів:
W = E P(i,j)*d(i,j) = P(1,2)*d(1,2) + P(1,18)*d(1,18) +
P(1,20)*d(1,20) + +P(2,4)*d(2,4) + P(2,6)*d(2,6) + P(3,4)*d(3,4) +
P(3,10)*d(3,10) + +P(4,5)*d(4,5) + P(4,10)*d(4,10) + P(5,6)*d(5,6) +
P(5,8)*d(5,8) + +P(5,9)*d(5,9) + P(5,10)*d(5,10)+ P(5,11)*d(5,11) +
P(6,7)*d(6,7) + +P(7,9)*d(7,9) + P(7,10)*d(7,10) + P(7,11)*d(7,11) +
P(7,12)*d(7,12) + +P(8,9)*d(8,9) + P(9,10)*d(9,10) + P(11,12)*d(11,12)
+P(12,13)*d(12,13) + +P(13,14)*d(13,14) + P(13,15)*d(13,15) + P(13,22)*d(13,22)
+
+P(14,17)*d(14,17) + P(15,17)*d(15,17) + P(15,19)*d(15,19)
+ +P(15,22)*d(15,22) +P(16,19)*d(16,19) + P(16,22)*d(16,22) +
+P(17,18)*d(17,18) + P(18,19)*d(18,19) +P(18,20)*d(18,20) + +P(19,20)*d(19,20)
+ P(19,21)*d(19,21) + P(20,22)*d(20,22) +
+P(21,22)*d(21,22) =
= 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*1
+1*1 + 1*2 + + 2*1 + 1*2 + 1*2 + 1*1 + 1*2 + 2*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*1
+ 1*1 + +1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*2 + 1*2 + 2*1 + 1*1 + 1*1 + 1*2 + 1*1
+ +1*1+ 1*2 + 1*2 = 53
Мінімальна можлива кількість переключень тригерів:
Wmin = E P(i,j) = 42
Коефіцієнт ефективності кодування: 1.26
2.1.4. Структурний синтез автомата на
підставі заданого типу тригерів
Таблиця переходів Т-тригера:
Табл.2. Таблиця переходів Т-тригера
|
Qt
|
Qt+1
|
T |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
На підставі цієї таблиці я вказую у табл.1 який тригер
встановиться в 1, а який в 0.
2.1.5. Функції збудження тригерів та
вихідних сигналів
Введемо слідуючі позначення:
А=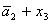 ; B= ; B=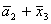 ;
C= ;
C=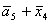 ; F= ; F=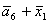 ;
G= ;
G=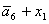 ; ;
L=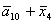 ; P= ; P=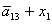 ; Q= ; Q=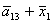 ; R= ; R=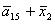 ; S= ; S=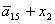 ; ;
T=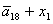 ; U= ; U=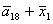 ; V= ; V=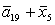 ; Б= ; Б=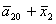 ; Y= ; Y=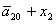 ; ;
Z=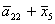 ; D= ; D=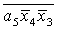 ; E= ; E=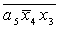 ; H= ; H=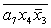 ; I= ; I=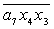 ; ;
J=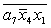 ; K= ; K=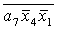 ; O= ; O=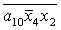 ; W= ; W=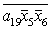 ; X= ; X=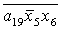 ; ;
Г=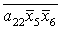 ; Д= ; Д=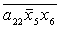 ;
M= ;
M=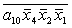 ; N= ; N=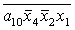 . .
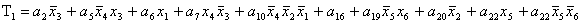 = =
=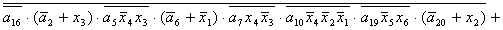
+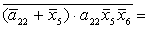 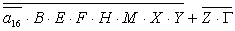 ; ;
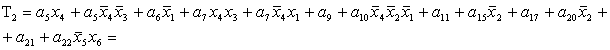
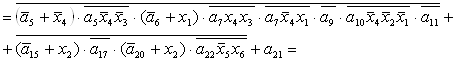 
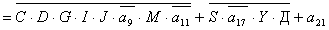 ; ;
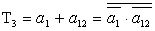 ; ;
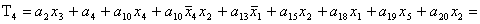
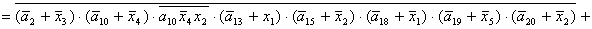  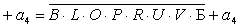 ; ;
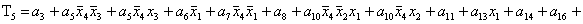 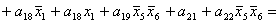
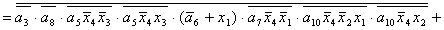
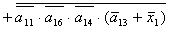 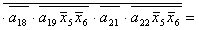
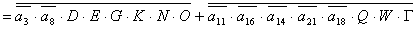 . .
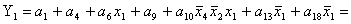
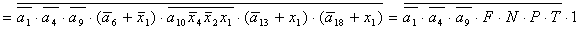 ; ;
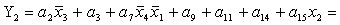
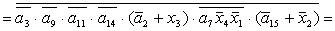 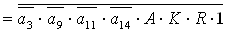 ; ;
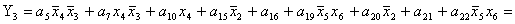
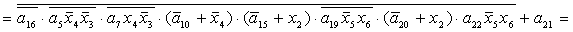
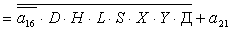 ; ;
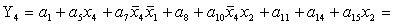
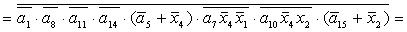
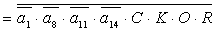 ; ;
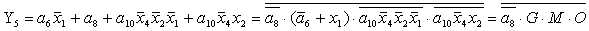 ; ;
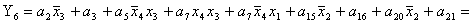
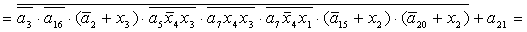
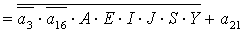 ; ;
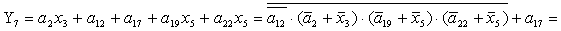
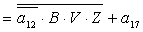 ; ;
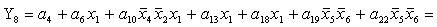
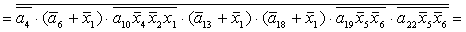
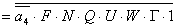 ; ;
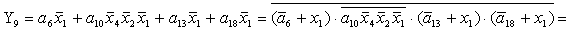
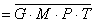 ; ;
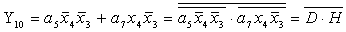 . .
2.2. Структурний синтез автомата Мура
2.2.1. Розмітка станів ГСА
Для автомата Мура на етапі одержання відміченої ГСА розмітка
провадиться відповідно до наступних правил:
1)
символом а1 відмічаються початкова і кінцева вершини;
2)
різні операторні вершини відмічаються різними символами;
3) всі операторні вершини повинні бути відмічені.
Відповідно до цих правил я відмітив 25 станів, які показан
на рис. 2.
2.2.2. Таблиця переходів автомата
Для кожного стану ai визначаю по ГСА всі шляхи, які ведуть в інші стани.
Я буду будувати зворотну таблицю переходів для автомата
Мура, тому що я синтезую автомат на базі D-тригера.
Табл.3. Таблиця переходів D-тригера
|
Am
as(Y)
Kas
Xamas
D1
D2
D3
D4
D5
|
a23 |
a24
a1(-)
00010
1
|
X2
D4
|
D4 |
U |
a12 |
a11
a2(Y1,Y2)
|
00100 |
1 |
| 1 |
D3 |
D3 |
|
|
|
a1
a3(Y1,Y4)
11000
1
D1
D2
|
a2
a4(Y3)
00111
X4
D3
D4
D5
A
|
a3
a5(Y7)
01011
X3
D2
D4
D5
B
|
a2
a6(Y4,Y5)
10011
X4X2
D1
D4
D5
C
|
| a3 |
a4
a7(Y2,Y6)
|
01000 |
X3 |
1
D2
|
D2 |
|
a2 |
a5 |
a6 |
|
a7
a8(Y1,Y8)
00000
X4X2X1
|
X1 |
1 |
1 |
a2 |
a5
a9(Y5,Y9)
10000
X4X2X1
|
X1
D1
|
D1
V
|
W |
a8
a10(Y4)
01110
X4
D2
D3
D4
D
|
|
a10
a11(Y4,Y5)
10110
1
D1
D3
D4
|
a8 |
a9
a12(Y3,Y10)
00011
X4X3
|
X4X3
D4
|
D4
D5
|
D5
E
|
F |
a8 |
a9 |
a9
a13(Y6)
00001
X4X3
|
| X4X3 |
X4X1 |
D5 |
D5 |
D5
X
|
|
a9 |
a13
a14(Y2,Y4)
00101
X4X1
|
1
D3
|
D3
D5
|
|
D5
G
|
a24 |
a25
a15(Y3,Y6)
01001
X2
|
1
D2
|
D2
D5
|
D5
H
|
|
a14 |
a15
a16(Y7)
10001
1
|
X5
D1
|
|
D1
D5
|
D5 |
I |
a16
a17(Y1,Y9)
11100
X1
D1
D2
D3
J
|
a15 |
a16
a18(Y8)
00100
X5X6
|
X1
D3
|
D3
D4
|
D4
K
|
L |
|
a15
a19(Y3)
10101
X5X6
D1
D3
D5
M
|
a17 |
a18
a20(Y2,Y4)
01010
1
|
X2
D2
|
D2
D4
|
D4 |
N |
a18 |
a19
a21(Y3,Y6)
10010
X2
|
1
D1
|
|
D1
D4
|
D4
O
|
a20 |
a21
a22(Y7)
01100
1
|
X5
D2
|
D2
D3
|
D3 |
P |
a22
a23(Y1,Y9)
01101
X1
D2
D3
D5
Q
|
a21 |
|
a22
a24(Y8)
10100
X5X6
|
X1D1 |
D1
D3
|
D3
R
|
S |
a21
a25(Y3)
11001
X5X6
D1
D2
D5
T
|
|
|
|
|
2.2.3.
Кодування станів
Кодування станів буде проводитися за таким алгоритмом:
1. Кожному стану
автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm,
рівне числу переходів у стан аm (Nm дорівнює числу появ аm
у поле таблиці ).
2. Числа N1,
N2, ..., Nm упорядковуються по убуванні.
3. Стан аs
з найбільшим Ns кодується кодом: , де R-кількість елементів
пам'яті. , де R-кількість елементів
пам'яті.
4. Наступні R станів
згідно списку пункту 2 кодуються кодами, що містять тільки одну 1:00 ... 01, 00
... 10, ... , 01 ... 00, 10 ... 00.
5. Для станів, що
залишилися, знову в порядку списку п.2. використовують коди з двома одиницями,
потім із трьома і так далі поки не будуть закодовані вес стани.
У результаті виходить таке кодування, при якому чим більше мається
переходів у деякий стан, тим менше одиниць у його коді. Вираження
для функцій збудження будуть простіше для D-тригерів, тому що
функції порушення однозначно визначаються кодом стану переходу.
Результати кодування за цим алгоритмом заношу до таблиці 3.
2.2.4. Структурний синтез автомата на
підставі заданого типу тригерів
Таблиця переходів D-тригера:
Табл.2. Таблиця переходів D-тригера
|
Qt
|
Qt+1
|
D |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
На підставі цієї таблиці я вказую у табл.1 який тригер
встановиться в 1, а який в 0.
2.2.5. Функції збудження тригерів та
вихідних сигналів
Введемо слідуючі позначення:
U=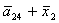 ; A= ; A=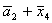 ;
B= ;
B=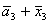 ; W= ; W=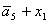 ;
D= ;
D=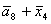 ; ;
H=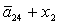 ; I= ; I=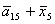 ; J= ; J=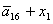 ; L= ; L=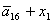 ; N= ; N=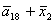 ; ;
O=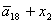 ; P= ; P=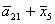 ; Q= ; Q=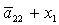 ; S= ; S=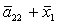 ; C= ; C=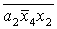 ; ;
E=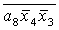 ; F= ; F=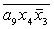 ; X= ; X=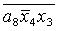 ; G= ; G=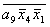 ; K= ; K=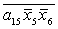 ; ;
M=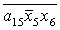 ; R= ; R=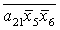 ; T= ; T=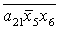 ; V= ; V=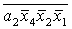 . .
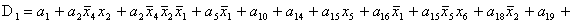
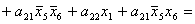
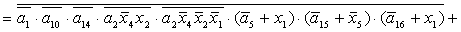
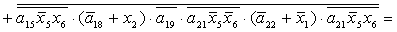
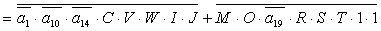 ; ;
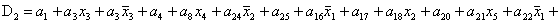
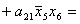
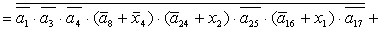
+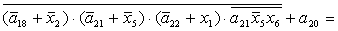
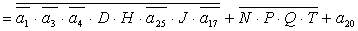 ; ;
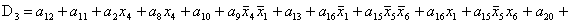
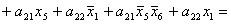
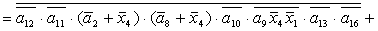
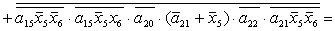
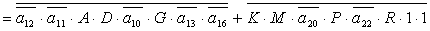 ; ;
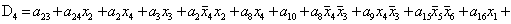
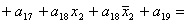
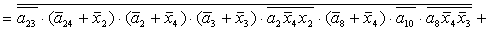
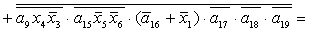
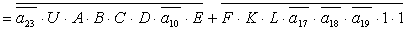 ; ;
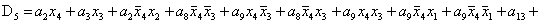
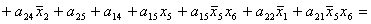
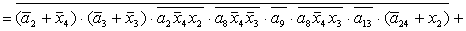
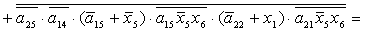
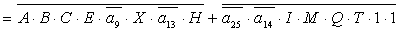 . .
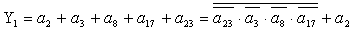 ; ;
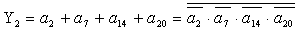 ; ;
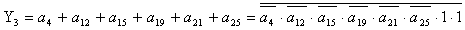 ; ;
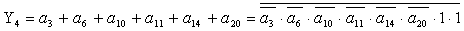 ; ;
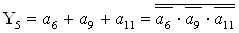 ; ;
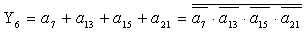 ; ;
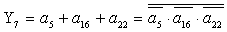 ; ;
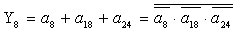 ; ;
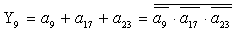 ; ;
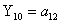 . .
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1.
Прикладная теория цифрових автоматов/К.Г.Самофалов,
А.М.Романкевич, В. Н. Валуйский и др.-К.:Вища шк.,1987.
2.
Савельєв А. Я. Прикладная теория цифрових
автоматов.-М.: Высш. шк.,1987.
3.
Справочник по интегральным микросхемам / Под ред.
Б. В. Тарабрина,-М.: Радио и связь, 1987.
4.
ГОСТ 2.708-81 ЕСКД. Правила выполнения электрических схем цифровой
вычислительной техники.
5.
ГОСТ 2.743-82 ЕСКД. Обозначения условные графические в схемах. Элементы
цифровой техники.
|


