Информатика программирование : Доклад: Проведение хроматографического анализа в условиях не полностью разделенных пиков

Доклад: Проведение хроматографического анализа в условиях не полностью разделенных пиков

Программа peak2

Немировский А.М.

При проведении хроматографического анализа часто встречаются случаи, в которых пики не полностью разделены, что оказывает влияние на точность проведения анализа. В предлагаемой вниманию работе, предлагается использовать расчет, который базируется на проведении модельных опытов с образцами, содержащими вещества известных концентраций, и измерении получившихся высот пиков. Далее делается предположение, что приращение пика от влияния пика-соседа пропорционально высоте пика-соседа.

Нанести на график результаты модельных экспериментов легко, но возникает вопрос о практическом использовании этого графика для уточнения результатов рабочих анализов, так как в обеих частях функции фигурирует неизвестная величина С, которую и надо определить. Эта проблема разрешается с помощью организации итерационного процесса, исходной посылкой которого является приближенная величина С/Сf .

Рассмотрим подробнее итерационный процесс. После того, как проведена калибровка, мы можем фактически располагать 2-мя графиками:

Предположим, что Cf/C=Hf/H. Пользуясь этим предположением, из первого уравнения находим С, а из второго - Сf. Далее вычислим отношение Сf/C, которое обладает лучшим приближением к истинным значениям, чем Hf/H. Затем полученные Cf и C подставляем в уравнение (2) и (3). Процесс таким образом можно продолжать далее до тех пор, пока не будет достигнута необходимая точность.

Для придания наглядности нашим рассуждениям, проведем показательные расчеты на математической модели. Пусть ситуацию с пересекающимися пиками создает следующая закономерность:

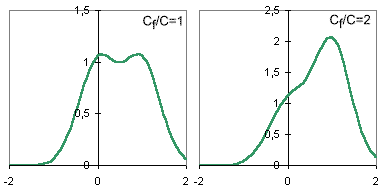
На рисунке 1 показаны графики этой функции при Cf/C равном 1 и 2. Второй график, очевидно, не имеет положенного первого максимума. В связи с этим мы будем считать точку перегиба максимумом второго пика.

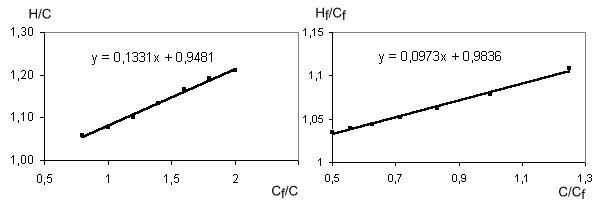
На рисунке 2 изображены графики функций (2) и (3), о которых мы говорили ранее. Из рисунка следует, что гипотеза о линейном влиянии соседнего пика на величину основного вполне применима. Безусловно, не надо пытаться включать в область линейности точки на большом интервале Cf/C, так как результаты аппроксимации будут неудовлетворительными. Об этом свидетельствуют различные параметры на вышеупомянутых графиках, тогда как они должны быть одинаковыми, поскольку форма моделируемых хроматографических пиков одинакова. Различные же параметры говорят о том, что аппроксимация проводилась в разных диапазонах Cf/C.

Прочитав этот материал, проницательный читатель сразу скажет: "А как этим пользоваться?" Измерять данные для калибровки, строить 2 графика, порождать итерационный процесс очень непросто! Для облегчения жизни я предлагаю вниманию собственную компьютерную программку, которая существенно упрощает процесс вычисления результатов анализа. Она называется Peak2. Понять принцип ее работы несложно, однако о некоторых ее свойствах я расскажу подробнее. Во-первых, программа позволяет проводить вычисления не только на линейных графиках, но и на нелинейных. Для работы в условиях нелинейности калибровки позволяет работать режим измерения "Ломаная линия". Из названия следует, что экспериментальные точки просто соединяются ломаной линией, что позволяет точнее получать результат в условиях нелинейной калибровки. Для того чтобы распознать недопустимую кривизну калибровки, существует режим "Совет", который знакомит с возможной максимальной систематической погрешностью при использовании линейной аппроксимации и позволяет выбрать необходимый режим расчетов. У программы Peak2 существует одно ограничение: нельзя вводить нулевые значения концентраций! Если таковые вводить, они не будут учитываться при расчетах.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.novedu.ru/